题目内容
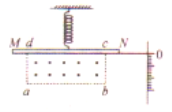
【题目】如图所示，在某竖直平面内，光滑曲面AB与水平面BC平滑连接于B点，BC右 端连接内壁光滑、半径
的四分之一细圆管CD，管口D端正下方直立一根劲度系数为
的轻弹簧，弹簧一端固定，另一端恰好与管口D端平齐。一个质量为
的小球放在曲面AB上，现从距BC的高度为
处静止释放小球，它与BC间的动摩擦因数
，小球进入管口C端时，它对上管壁有
的相互作用力，通过CD后，在压缩弹簧过程中滑块速度最大时弹簧的弹性势能为
，取重力加速度
。求：
（1）小球在C处受到的向心力大小；
（2）在压缩弹簧过程中小球的最大动能
；
（3）小球最终停止的位置.
【答案】(1) 
(2) 
(3) 
【解析】⑴小球进入管口C端时它与圆管上管壁有大小为
的相互作用力
故小球受到的向心力为：
⑵在C点，由
，代入数据得： 
在压缩弹簧过程中，速度最大时，合力为零，设此时滑块离D端的距离为
则有
解得
设最大速度位置为零势能面，由机械能守恒定律有
得
⑶滑块从A点运动到C点过程，由动能定理得
，解得BC间距离
小球与弹簧作用后返回C处动能不变，小滑块的动能最终消耗在与BC水平面相互作用的过程中，设物块在BC上的运动路程为
，由动能定理有
，解得
故最终小滑动距离B为
处停下.
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
