Question

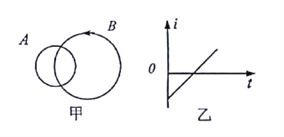
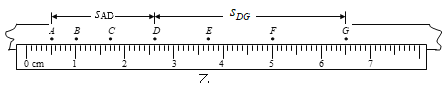
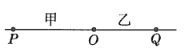
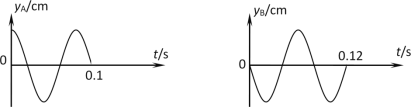
【题目】如图所示，甲、乙是两条不同材料的弹性细绳，两绳在处连接。分别是甲乙两绳上的两点距为，间距为。点上下振动时形成向左、向右传播的简谐横波。时刻点处在波谷位置。后波谷恰好传播到点，此时间还有一个波谷，且点在平衡位置且向上运动。已知乙波的波速为。则下列说法正确的是（　　）

A.甲波的波长为

B.甲波的波速为

C.点的振动周期为

D.时，点恰好处于波谷

E.当点处于波峰时，点也一定处于波峰

Answer 1

【答案】BCE

【解析】

A．由后的波形特点知

则

故A错误；

BC．甲波的波速

则甲波的周期

。

波的频率等于波源的振动频率，则甲、乙两波频率相等，则其周期相等，则有

故BC正确；

D．乙波波长

则有

则时刻点处于平衡位置向下振动。再经过时间

点在波峰，故D错误；

E．两点距离波源均为各自波长的倍，又二者振动周期相同、起振方向相同，则二者振动步调相同，当点处在波峰时，点也一定处在波峰，故E正确。

故选BCE。