��Ŀ����
����Ŀ����ͼ�������������õı���ԲͲ����������ֱ�����ط���ˮ�У�Ͳ�ڷ����һ�����������壨����Ϊ�������壩����Ͳ����ˮ����ƽʱ��ԲͲǡ�þ�ֹ��ˮ�У���ʱˮ���¶�t1=7.0�棬Ͳ�������ij���h1=14cm����֪����ѹǿp0=1.0��105Pa��ˮ���ܶȦ�=1.0��103kg/m3 �� �������ٶȴ�Сgȡ10m/s2 �� 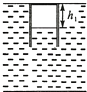
����������ˮ�»���������27�棬��ʱͲ��¶��ˮ��ĸ߶ȡ�hΪ���٣�
��������ˮ������27��ֲ��䣬������ԲͲ����������ijһλ�ã���ȥ������ԲͲǡ�ܾ�ֹ�����ʱͲ��ˮ��ľ���H�����������λ��Ч���֣���
���𰸡��⣺��i����ԲͲ�ĺ�����ΪS��ˮ������27��ʱ�������ij���Ϊh2�����ݸ������˶����� ![]() ��
��
ԲͲ��ֹ��Ͳ����Һ��߶Ȳ�䣬�С�h=h2��h1��
�ɢ٢�ʽ�á�h=1cm��
��ii����ԲͲ������Ϊm����ֹ��ˮ��ʱͲ�������ij���Ϊh3�����gh1S=mg ��gh3S=mg��
ԲͲ�ƶ����̣����ݲ���������У�p0+��gh1��h2S=[p0+��g��H+h3��]h3S��
�ɢܢ�ʽ�� H=1.7cm��
�𣺣���������ˮ�»���������27�棬��ʱͲ��¶��ˮ��ĸ߶ȡ�hΪ1cm
��������ˮ������27��ֲ��䣬������ԲͲ����������ijһλ�ã���ȥ������ԲͲǡ�ܾ�ֹ����ʱͲ��ˮ��ľ���HΪ1.7cm��
����������1���¶����ߵĹ����з�����ѹ�仯��������������״̬����������ʽ��⡣
��2��ԲͲ�������Ʒ����ĵ��±仯��������������״̬����������⼴�ɡ�

 �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�