题目内容
如图所示,压路机后轮的半径是前轮半径的3倍,A、B分别为前轮和后轮边缘上的一点,C为后轮上一点,它离后轮轴的距离是后轮半径的一半,即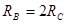 ,
,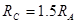 ,
,
则A、B、C三点的角速度和向心加速度的比值分别为
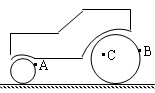
A.3∶1∶1; 9∶2∶1 B.3∶1∶1;6∶2∶1
C.1∶3∶3; 2∶6∶3 D.1∶3∶3; 6∶2∶1
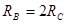 ,
,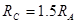 ,
,则A、B、C三点的角速度和向心加速度的比值分别为

A.3∶1∶1; 9∶2∶1 B.3∶1∶1;6∶2∶1
C.1∶3∶3; 2∶6∶3 D.1∶3∶3; 6∶2∶1
B
考点:
专题:匀速圆周运动专题.
分析:传动装置,在传动过程中不打滑,则有:共轴的角速度是相同的;同一传动装置接触边缘的线速度大小是相等的.所以当角速度一定时,线速度与半径成正比;当线速度大小一定时,角速度与半径成反比.因此根据题目条件可知三点的线速度及角速度关系.
解答:解:A、B分别为同一传动装置前轮和后轮边缘上的一点,所以VA=VB,因为rA:rB=1:3,
所以ωA:ωB=3:1;B、C两点共轴,所以ωC=ωB .所以ωA:ωB:ωC=3:1:1;
向心加速度a=ω2r,所以aA:aB:aC=6:2:1
故选B.
点评:本题要紧扣隐含条件:共轴的角速度是相同的;同一传动装置接触边缘的线速度大小是相等的.以此作为突破口;同时能掌握线速度、角速度与半径之间的关系.
专题:匀速圆周运动专题.
分析:传动装置,在传动过程中不打滑,则有:共轴的角速度是相同的;同一传动装置接触边缘的线速度大小是相等的.所以当角速度一定时,线速度与半径成正比;当线速度大小一定时,角速度与半径成反比.因此根据题目条件可知三点的线速度及角速度关系.
解答:解:A、B分别为同一传动装置前轮和后轮边缘上的一点,所以VA=VB,因为rA:rB=1:3,
所以ωA:ωB=3:1;B、C两点共轴,所以ωC=ωB .所以ωA:ωB:ωC=3:1:1;
向心加速度a=ω2r,所以aA:aB:aC=6:2:1
故选B.
点评:本题要紧扣隐含条件:共轴的角速度是相同的;同一传动装置接触边缘的线速度大小是相等的.以此作为突破口;同时能掌握线速度、角速度与半径之间的关系.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
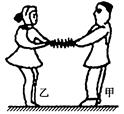
 的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是
的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是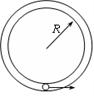
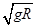
 ,则此时小球给管道壁有竖直向下作用力
,则此时小球给管道壁有竖直向下作用力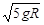 ,则此时小球给管道间的相压大小为6mg
,则此时小球给管道间的相压大小为6mg
 是电动机皮带轮半径的3倍(如图),皮带与两轮之间不发生滑动
是电动机皮带轮半径的3倍(如图),皮带与两轮之间不发生滑动 。已
。已 知
知 机器皮带轮边缘上一点的向心加速度为0.10 m/s2。
机器皮带轮边缘上一点的向心加速度为0.10 m/s2。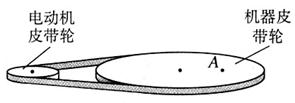
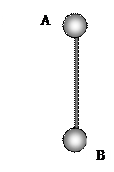
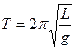 ,求直杆转到如图所示竖直位置时,A、B两球对直杆作用力各多大?方向如何?
,求直杆转到如图所示竖直位置时,A、B两球对直杆作用力各多大?方向如何? 
 m/s时对桥的压力的大小;
m/s时对桥的压力的大小;