题目内容
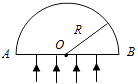
【题目】水平地面上有质量分别为m和4m的物A和B，两者与地面的动摩擦因数均为μ．细绳的一端固定，另一端跨过轻质动滑轮与A相连，动滑轮与B相连，如图所示．初始时，绳处于水平拉直状态．若物块A在水平向右的恒力F作用下向右移动了距离s，重力加速度大小为g．求
（1）物块B克服摩擦力所做的功；
（2）物块A、B的加速度大小．
【答案】
（1）
解：物块A移动了距离s，则物块B移动的距离为
s1= 
①
物块B受到的摩擦力大小为
f=4μmg②
物块B克服摩擦力所做的功为
W=fs1=4μmg× 
s=2μmgs
（2）
解：设物块A、B的加速度大小分别为aA、aB，绳中的张力为T．有牛顿第二定律得
F﹣μmg﹣T=maA④
2T﹣4μmg=4maB⑤
由A和B的位移关系得
aA=2aB⑥
联立④⑤⑥式得
aA= 
⑦
aB= 
⑧
【解析】（1）根据几何关系确定B的位移；再根据滑动摩擦力公式可明确摩擦力的大小，根据功的公式即可求得克服摩擦力所做的功；（2）分别对AB受力分析，根据牛顿第二定律进行列式，联立可求得两物体的加速度．
【考点精析】认真审题，首先需要了解恒力做功(恒力的功可根据W=F·S·cosθ进行计算，本公式只适用于恒力做功)．
练习册系列答案
相关题目
