题目内容
将一个动力传感器连接到计算机上，我们就可以测量快速变化的力，某一小球用一条不可伸长的轻绳连接，绳的另一端固定在悬点上，当小球在竖直面内来回摆动时，用动力传感器测得绳
子对悬点的拉力随时间变化的曲线如图所示，取重力加速度g=10m/s2，求绳子的最大偏角θ。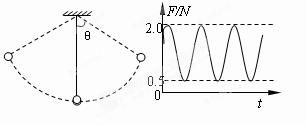
绳子的最大偏角θ=600
解析试题分析:设小球的质量为m，绳子长度为L，绳子拉力的最小值和最大值各为F1和F2，小球摆至最高点时，绳子拉力最小F1="mgCosθ" （1）
小球摆至最低点时，绳子拉力最大F2—mg=m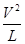
（2）
摆动过程小球机械能守恒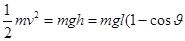
）（3）
由以上各式得：cosθ=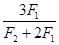
=0.5 （4）2分 θ=600 （5）
考点： 机械能守恒定律，向心力公式
练习册系列答案
相关题目
如图所示，圆心在O点、半径为R的圆弧轨道abc竖直固定在水平桌面上，Oc与Oa的夹角为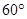
，轨道最低点a与桌面相切。一轻绳两端系着质量为m1和m2的小球（均可视为质点），挂在圆弧轨道边缘c的两边，开始时，m1位于c点，然后从静止释放，设轻绳足够长，不计一切摩擦。则（ ）
| A．在m1由c下滑到a的过程中，两球速度大小始终相等 |
| B．m1在由c下滑到a的过程中重力的功率先增大后减小 |
| C．若m1恰好能沿圆弧轨道下滑到a点，则m1=3m2 |
| D．若m1恰好能沿圆弧轨道下滑到a点，则m1=2m2 |
小球距坐标原点O的距离s为多远？
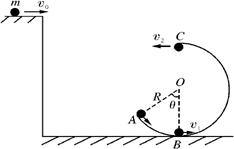
的圆弧状的曲面，已知重力加速度为 g＝10m／s2，求：