题目内容
【题目】如图所示,光滑平行导轨倾斜放置,导轨平面倾角为θ=30°,导轨间距为L,导轨上端接有阻值为R的定值电阻,整个装置处在垂直导轨平面向上的匀强磁场中,磁场的磁感应强度大小为B,一根金属棒放在导轨上,由静止释放,同时给金属棒施加一个沿导轨平面向下的拉力,使金属棒以大小为a=0.5g的加速度向下做匀加速运动,g为重力加速度,金属棒运动过程中始终与导轨垂直并接触良好,不计导轨和金属棒的电阻,金属棒运动t时间时,金属棒两端的电压U、t时间内通过电阻R的电量q、拉力做功的瞬时功率P、电阻R产生的焦耳热Q随时间变化正确的是( )
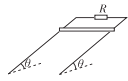
A.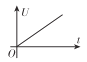 B.
B.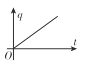
C.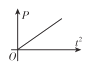 D.
D.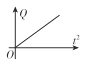
【答案】AC
【解析】
A.由题意可知金属棒两端的电压等于产生的电动势:
![]()
因为金属棒向下做匀加速运动,故金属棒两端的电压与时间成正比,故A正确;
B.根据:
![]()
![]()
![]()
可得:
![]()
可知通过电阻R的电量q与t成二次函数关系,故B错误;
C.因为金属棒向下做匀加速运动,根据牛顿第二定律有:
![]()
a=0.5g
又因为:
![]()
联立可得:
![]()
拉力做功的瞬时功率为:
![]()
可知与t2成正比关系,故C正确;
D.电阻R产生的焦耳热根据焦耳定律有:
![]()
可知Q与t2不成一次函数关系,故D错误。
故选AC。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目