题目内容
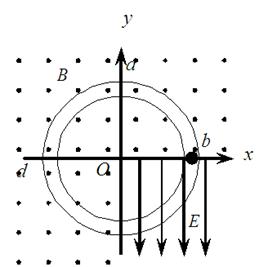
(19分)如图,在区域I(0≤x≤d)和区域II(d≤x≤2d)内分别存在匀强磁场,磁感应强度大小分别为B和2B,方向相反,且都垂直于Oxy平面。一质量为m、带电荷量q(q>0)的粒子a于某时刻从y轴上的P点射入区域I,其速度方向沿x轴正向。已知a在离开区域I时,速度方向与x轴正方向的夹角为30°;此时,另一质量和电荷量均与a相同的粒子b也从p点沿x轴正向射入区域I,其速度大小是a的1/3。不计重力和两粒子之间的相互作用力。求
(1)粒子a射入区域I时速度的大小;
(2)当a离开区域II时,a、b两粒子的y坐标之差。
(1)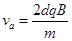 (2)
(2)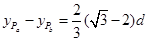
解析试题分析:(1)设粒子a在I内做匀速圆周运动的圆心为C(在y轴上),半径为Ra1,粒子速率为va,运动轨迹与两磁场区域边界的交点为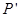 ,如图。由洛仑兹力公式和牛顿第二定律得
,如图。由洛仑兹力公式和牛顿第二定律得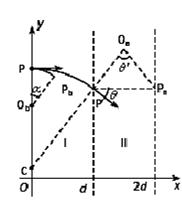
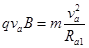 (1)
(1)
由几何关系得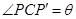 (2)
(2) (3)
(3)
式中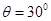
由(1)(2)(3)式得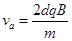 (4)
(4)
(2)设粒子在II区内做圆周运动的的圆心为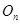 ,半径为
,半径为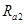 ,射出点为
,射出点为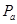 (图中末画出轨迹)
(图中末画出轨迹)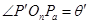
由洛仑兹力分式和牛顿第二定律得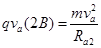 (5)
(5)
由(1)(5)式得: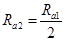 (6)
(6)
C,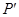 和
和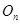 三点共线,且由(6)式知
三点共线,且由(6)式知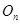 必位于
必位于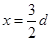 (7)
(7)
的平面上,由对称性知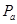
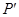 纵坐标相同,即
纵坐标相同,即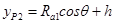 (8)
(8)
式中h是C点的Y坐标
设b在I中运动的轨道半径为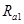 ,由洛仑兹力公式和牛顿第二定律得
,由洛仑兹力公式和牛顿第二定律得 (9)
(9)
设a到达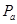 点时,b位于
点时,b位于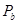 点,转过的角度为α。如果b没有飞出I,则
点,转过的角度为α。如果b没有飞出I,则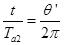 (10)
(10)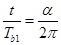 (11)
(11)
式中,t是a在区域II中运动的时间,而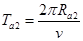 (12)
(12)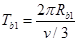 (13)
(13)
由⑤⑨⑩(11)(12)(13)式得 (14)
(14)
由①③⑨(14)式可见,b没有飞出I。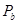 点的y坐标为
点的y坐标为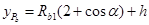 (15)
(15)
由(1)(3)(8)(9)(14)(15)式及题给条件得,a、b两粒子的y坐标之差为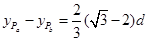 (16)
(16)
考点:牛顿第二定律,带电粒子在电磁场中的运动

如图所示,把小车放在倾角为30°的光滑斜面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,不计滑轮质量及摩擦,已知小车的质量为3m,小桶与沙子的总质量为m,小车从静止释放后,在小桶上升竖直高度为h的过程中( )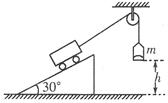
| A.小桶处于失重状态 | B.小桶的最大速度为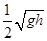 |
| C.小车受绳的拉力等于mg | D.小车的最大动能为mgh |
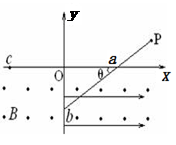
如图所示,在第二象限内有水平向右的匀强电场,电场强度为E,在第一、第四象限内分别存在如图所示的匀强磁场,磁感应强度大小相等. 有一个带电粒子以初速度v0垂直x轴,从x轴上的P点进入匀强电场,恰好与y轴成45°角射出电场,再经过一段时间又恰好垂直于x轴进入下面的磁场.已知OP之间的距离为d,则带电粒子( )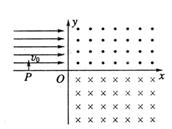
A.在电场中运动的时间为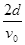 |
B.在磁场中做圆周运动的半径为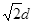 |
C.自进入磁场至第二次经过x轴所用时间为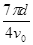 |
D.自进入电场至在磁场中第二次经过x轴的时间为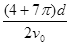 |
在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场,如图.PQ为两个磁场的边界,磁场范围足够大.一个边长为a、质量为m、电阻为R的金属正方形线框,以速度2v垂直磁场方向从如图实线(I)位置开始向右运动,当线框运动到分别有一半面积在两个磁场中的如图(II)位置时,线框的速度为v,则下列说法正确的是
A.图(II)时线框中的电功率为 |
B.此过程中回路产生的电能为 |
C.图(II)时线框的加速度为 |
D.此过程中通过线框截面的电量为 |


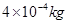 带电量为q=+
带电量为q=+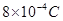 的带电小球,从小孔P以速度v=2m/s水平射入上述电场、磁场区域,之后从OA板上的M点垂直OA方向飞出上述的电磁场区域后而进入下方的电磁场区域 ,OA板下方电场方向变为水平向右,电场强度大小为
的带电小球,从小孔P以速度v=2m/s水平射入上述电场、磁场区域,之后从OA板上的M点垂直OA方向飞出上述的电磁场区域后而进入下方的电磁场区域 ,OA板下方电场方向变为水平向右,电场强度大小为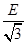 ,当小球碰到水平地面时立刻加上匀强磁场,磁感应强度大小仍为B=1T,方向垂直纸面向里。小球与水平地面相碰时,竖直方向速度立刻减为零,水平方向速度不变,小球运动到D处刚好离开水平地面,然后沿着曲线DQ运动,重力加速度为g=10m/s2,小球在水平地面上运动过程中电量保持不变,不计摩擦。
,当小球碰到水平地面时立刻加上匀强磁场,磁感应强度大小仍为B=1T,方向垂直纸面向里。小球与水平地面相碰时,竖直方向速度立刻减为零,水平方向速度不变,小球运动到D处刚好离开水平地面,然后沿着曲线DQ运动,重力加速度为g=10m/s2,小球在水平地面上运动过程中电量保持不变,不计摩擦。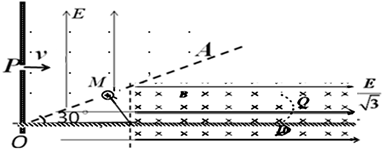
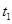 ;
;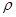 (即把那一段曲线尽可能的微分,近似一个圆弧,这个圆弧对应的半径即曲线上这个点的曲率半径)。求vm与
(即把那一段曲线尽可能的微分,近似一个圆弧,这个圆弧对应的半径即曲线上这个点的曲率半径)。求vm与