��Ŀ����
13�� ������ͼװ�á���֤����ƽ���ı��ζ���ʵ��ʱ��
������ͼװ�á���֤����ƽ���ı��ζ���ʵ��ʱ���ٳ����е����ģ���ľ�塢��ֽ�����ɳӡ�ϸ���ף�����������Ƥ�����̶ȳߡ���������ͼ����Ǧ�ʣ��⣬�����������ǰ壮
��ͬѧ���ڲ������������������ۣ����жԼ�Сʵ����������˵����AD��������ĸ���ţ�
A�����ɳӡ�ϸ������Ƥ����Ӧ��ľ��ƽ��
B����ϸ��֮��ļн�Խ��Խ��
C���������ɳ�ͬʱ��ϸ��ʱ�����ɳ�ʾ��֮��Ӧ�����ܴ�
D������Ƥ����ϸ��Ҫ��Щ�����ͬһϸ�����������ҪԶЩ
�۵��ɲ����Ƶ�ָ����ͼ��ʾ����ͼ��֪�����Ĵ�СΪ4.00N��
����ʵ���У������ϸ��Ҳ������Ƥ���ôʵ�����Ƿ�ᷢ���仯���𣺲��䣮��ѡ��䡱���䡱��
���� ��̽���������ϳɵĹ���ʵ�飺������������������Ƥ����һ��������Ƥ������������Ч����ͬ������������Ĵ�С�ͷ����Լ�һ�����Ĵ�С�ͷ���������ͼʾ����������������ƽ���ı��������������ĺ���������ֵ������һ������ʵ��ֵ�����бȽϣ���ƽ���ı��λ�������������ֵ������Ƥ��ͬ�ߵ��Ǹ���ʵ��ֵ��
��� �⣺��1����̽���������ϳɵĹ���ʵ�飺������������������Ƥ����һ��������Ƥ������������Ч����ͬ������������Ĵ�С�ͷ����Լ�һ�����Ĵ�С�ͷ���������ͼʾ����������������ƽ���ı��������������ĺ���������ֵ������һ�������бȽϣ�
����������Ҫ��ʵ�������У���ľ�壨�̶���ֽ������ֽ����¼����ͼ�����̶ȳߣ�ѡ��ȣ������ף����ɳ�����Ƥ���������ɲ����ƣ������Ĵ�С����ͼ�����̶���ֽ�������ǰ壨��ƽ���ı��Σ�����Ƥ��������������ͬ������Ч���ģ���
���Ի����������ǰ壮
��2��A����������ʵ��Ҫ����ȷ��Ϊ�˼�Сʵ������Ħ����ɵ���������Ҫ�ɳӡ�ϸ������Ƥ����Ӧ��ľ��ƽ�У���A��ȷ��
B������ϸ���ļнDz���Խ��Խ�ã��Է�����ƽ���ı���Ϊ�ˣ���B����
C���õ��ɳ�ͬʱ��ϸ��ʱ����������̫̫��Ҳ����̫С����C����
D��Ϊ�˸���ȷ�ļ�¼���ķ�������Ƥ����ϸ��Ҫ��Щ�����ͬһϸ�����������ҪԶЩ����D��ȷ��
��ѡ��AD
��3�����ɲ����Ƶ�ָ����ͼ��ʾ����ͼ��֪�����Ĵ�СΪ4.00 N��
��4�������ϸ��Ҳ������Ƥ�ֻҪ�����������ͬ��λ�ã�ʵ�������ᷢ���仯��
�ʴ�Ϊ�������ǰ� ��AD ��4.00 �ܲ���
���� �ڡ���֤����ƽ���ı��ζ���ʵ���У�����Ҫ֪�������ͺ�����Ч���ǵ�ͬ�ģ���Ҫ��ͬѧ�Ƕ��ڻ���֪ʶҪ�������ղ�����ȷӦ�ã���ǿ�Ի���ʵ�����⣮

 ij��ȤС������һС�ͷ������ʹ��Ȧ����ǿ�ų����ƴ�ֱ�ڴų�����Ĺ̶���ת����������Ȧ�Ĵ�ͨ������ʱ��t�����ҹ��ɱ仯��ͼ����ͼ��ʾ����Ȧת������ΪT����Ȧ�����ĵ綯�Ƶ����ֵΪEm��������˵��������ǣ�������
ij��ȤС������һС�ͷ������ʹ��Ȧ����ǿ�ų����ƴ�ֱ�ڴų�����Ĺ̶���ת����������Ȧ�Ĵ�ͨ������ʱ��t�����ҹ��ɱ仯��ͼ����ͼ��ʾ����Ȧת������ΪT����Ȧ�����ĵ綯�Ƶ����ֵΪEm��������˵��������ǣ�������| A�� | ��t=$\frac{T}{4}$ʱ���ų���������Ȧƽ��ƽ�� | |
| B�� | ��t=$\frac{T}{2}$ʱ����Ȧ�еĴ�ͨ���仯����� | |
| C�� | ��Ȧ�е綯�Ƶ�˲ʱֵe=Emsin��$\frac{2��t}{T}$�� | |
| D�� | ����Ȧת������Ϊԭ����2��������Ȧ�е綯�Ʊ�Ϊԭ����4�� |
| A�� | nT | B�� | $\frac{T}{n}$ | C�� | T$\sqrt{n}$ | D�� | $\frac{T}{\sqrt{n}}$ |
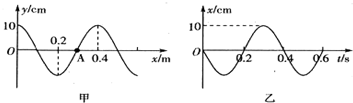
| A�� | ���в���x�Ḻ���� | |
| B�� | ���в��IJ��ٴ�СΪ1m/s | |
| C�� | ���˲�������һ�м�г��ɲ������ȶ������������������IJ���Ƶ��Ϊ0.4Hz | |
| D�� | ���ò�����һ�ϰ���������Ե�������������ϰ���ijߴ��40cm�����С | |
| E�� | �Ӹ�ʱ�����پ���0.4s��ʱ�䣬�ʵ�Aͨ����·��Ϊ40cm |
 ��ͼ��ʾ��R1Ϊ��ֵ���裬R2Ϊ�����ֵΪ2R1�Ŀɱ���裮EΪ��Դ�綯�ƣ�rΪ��Դ���裬��СΪr=R1����R2�Ļ�����P��a����b�Ĺ����У�����˵����ȷ���ǣ�������
��ͼ��ʾ��R1Ϊ��ֵ���裬R2Ϊ�����ֵΪ2R1�Ŀɱ���裮EΪ��Դ�綯�ƣ�rΪ��Դ���裬��СΪr=R1����R2�Ļ�����P��a����b�Ĺ����У�����˵����ȷ���ǣ�������| A�� | ����R2�Ĺ�����������С | |
| B�� | ��Դ�����������������С | |
| C�� | ��ѹ��ʾ���͵�����ʾ��֮�������� | |
| D�� | ��ѹ��ʾ���ı仯���͵�����ʾ���ı仯��֮�ȱ��ֲ��� |
| A�� | $\frac{v_1}{v_2}=\frac{r}{R}��\frac{a_1}{a_2}=\frac{r}{R}$ | B�� | $\frac{v_1}{v_2}=\sqrt{\frac{r}{R}}��\frac{a_1}{a_2}=\frac{r^2}{R^2}$ | ||
| C�� | $\frac{v_1}{v_2}=\sqrt{\frac{R}{r}}��\frac{a_1}{a_2}=\frac{R^2}{r^2}$ | D�� | $\frac{v_1}{v_2}=\frac{R}{r}��\frac{a_1}{a_2}=\frac{R}{r}$ |
 ��ͼ��ʾ������ˮƽ�����ϵ�ľ��A���ھ�ֹ״̬�����ҵ���������̵�������Ϊ0.6kg�����ɳӴ�ʱ�Ķ���Ϊ2N��������ȡ�����еIJ������룬ʹ��������̵����������ٵ�0.3kg����ô��װ�ý�����ֵ�����ǣ�g=10m/s2�����ƻ���Ħ������������
��ͼ��ʾ������ˮƽ�����ϵ�ľ��A���ھ�ֹ״̬�����ҵ���������̵�������Ϊ0.6kg�����ɳӴ�ʱ�Ķ���Ϊ2N��������ȡ�����еIJ������룬ʹ��������̵����������ٵ�0.3kg����ô��װ�ý�����ֵ�����ǣ�g=10m/s2�����ƻ���Ħ������������| A�� | ���ɳӵĶ�������С | B�� | ľ��A�Դ��ھ�ֹ״̬ | ||
| C�� | ľ��A�������Ħ�������� | D�� | ľ��A���ܵĺ�����Ҫ��� |
 ��ͼ��ʾ������ΪM��ľ��A���ڴֲڵ�ˮƽ���ϣ�����Ϊm��С��ͨ������ľ��A������������ˮƽ�����a�ǵ�б���ϵĺ���F����С�����ľ��һ�������˶�����M��m���λ�ñ��ֲ���ʱ��������ˮƽ�˼�ļн�Ϊ�ȣ���֪ľ��A��ˮƽ�˼�Ķ�ĥ�������̣���
��ͼ��ʾ������ΪM��ľ��A���ڴֲڵ�ˮƽ���ϣ�����Ϊm��С��ͨ������ľ��A������������ˮƽ�����a�ǵ�б���ϵĺ���F����С�����ľ��һ�������˶�����M��m���λ�ñ��ֲ���ʱ��������ˮƽ�˼�ļн�Ϊ�ȣ���֪ľ��A��ˮƽ�˼�Ķ�ĥ�������̣���