题目内容
5. 如图所示,质量为M的木块A套在粗糙的水平杆上,质量为m的小球通过绳与木块A相连,今用与水平方向成a角的斜向上的恒力F拉着小球带动木块一起向右运动,当M、m相对位置保持不变时,轻绳与水平杆间的夹角为θ,已知木块A与水平杆间的动磨擦因数μ,求:
如图所示,质量为M的木块A套在粗糙的水平杆上,质量为m的小球通过绳与木块A相连,今用与水平方向成a角的斜向上的恒力F拉着小球带动木块一起向右运动,当M、m相对位置保持不变时,轻绳与水平杆间的夹角为θ,已知木块A与水平杆间的动磨擦因数μ,求:(1)轻绳的拉力大小;
(2)木块A的加速度的大小.
分析 (1)以小球为研究对象,根据竖直方向力平衡,求解轻绳的拉力大小.
(2)以整体为研究对象求出整体加速度的表达式,根据牛顿第二定律求解木块A的加速度.
解答 解:(1)设轻绳的拉力大小为T.
以小球m为研究对象有:
竖直方向有:Tsinθ+Fsinα=mg
可得 T=$\frac{mg-Fsinα}{sinθ}$
(2)设木块A的加速度为a.
对于m、M组成的系统,由牛顿第二定律得:
水平方向有:Fcosα-f=(M+m)a
竖直方向有:N+Fsinα-(M+m)g=0
又 f=μN
联立解得 a=$\frac{Fcosα-μ(Mg+mg-Fsinα)}{M+m}$
答:
(1)轻绳的拉力大小为$\frac{mg-Fsinα}{sinθ}$;
(2)木块A的加速度的大小为$\frac{Fcosα-μ(Mg+mg-Fsinα)}{M+m}$.
点评 本题掌握用整体法和隔离法分析组合体的受力,要灵活选择研究对象,抓住加速度相等条件是正确解题关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
15.铁路弯道处,内外轨组成的斜面与水平地面倾角为θ,当火车以某一速度v通过该弯道时,内、外轨恰不受侧压力作用,则下面说法正确的是( )
| A. | 转弯半径R=$\frac{{v}^{2}}{gsinθ}$ | |
| B. | 若火车速度大于v时,外轨将受到侧压力作用,其方向平行轨道平面向外 | |
| C. | 若火车速度小于v时,外轨将受到侧压力作用,其方向平行轨道平面向内 | |
| D. | 当火车质量改变时,安全速率也将改变 |
20.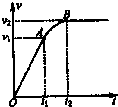 质量为m的汽车在平直的路面上启动,启动过程的速度图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行横轴的直线.已知从t1时刻开始汽车的功率保持不变.整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )
质量为m的汽车在平直的路面上启动,启动过程的速度图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行横轴的直线.已知从t1时刻开始汽车的功率保持不变.整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )
 质量为m的汽车在平直的路面上启动,启动过程的速度图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行横轴的直线.已知从t1时刻开始汽车的功率保持不变.整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )
质量为m的汽车在平直的路面上启动,启动过程的速度图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行横轴的直线.已知从t1时刻开始汽车的功率保持不变.整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )| A. | 0-t1时间内,汽车牵引力的数值为m$\frac{v_1}{t_1}$ | |
| B. | t1-t2时间内,汽车的功率等于(m$\frac{{v}_{1}}{{t}_{1}}$+Ff)v2 | |
| C. | tl-t2时间内,汽车的平均速率小于$\frac{{v}_{1}+{v}_{2}}{2}$v2 | |
| D. | 汽车运动的最大速率v2=($\frac{m{v}_{1}}{{F}_{f}{t}_{1}}$+1)v1 |
10.从地面竖直上抛一球,不计空气阻力,经时间t到达最高点,则小球运动到t-1和t+1两个时刻.( )
| A. | 位移相同 | B. | 加速度相同 | C. | 速度相同 | D. | 动能增量相同 |
6.以下实验中可以用打点计时器和纸带测速度进行数据处理的有 ( )
| A. | 验证牛顿运动定律 | B. | 验证力的平行四边形定则 | ||
| C. | 探究动能定理 | D. | 验证机械能守恒定律 |
3. 两个质量为m的圆环,套在水平的杆上,下端用两根等长的细线拴一质量为M的物体,如图所示,物体和圆环均处于静止状态,当圆环间的距离变大时,下列说法正确的是( )
两个质量为m的圆环,套在水平的杆上,下端用两根等长的细线拴一质量为M的物体,如图所示,物体和圆环均处于静止状态,当圆环间的距离变大时,下列说法正确的是( )
 两个质量为m的圆环,套在水平的杆上,下端用两根等长的细线拴一质量为M的物体,如图所示,物体和圆环均处于静止状态,当圆环间的距离变大时,下列说法正确的是( )
两个质量为m的圆环,套在水平的杆上,下端用两根等长的细线拴一质量为M的物体,如图所示,物体和圆环均处于静止状态,当圆环间的距离变大时,下列说法正确的是( )| A. | 杆对环的弹力保持下变 | B. | 圆环受的摩擦力变大 | ||
| C. | 绳中张力保持不变 | D. | 两张力的合力保持不变 |
4.静止的氡核${\;}_{86}^{222}$Rn放出α粒子后变成钋核${\;}_{84}^{218}$Po,α粒子动能为E0.若衰变放出的能量全部变为反冲核和α粒子的动能,真空中的光速为c,则该反应中的质量亏损为( )
| A. | $\frac{4{E}_{0}}{218{c}^{2}}$ | B. | 0 | C. | $\frac{222{E}_{0}}{218{c}^{2}}$ | D. | $\frac{218{E}_{0}}{222{c}^{2}}$ |
 如图,竖直圆筒固定不动,粗筒的横截面积是细筒的3倍,细筒足够长.粗筒中A,B两轻质活塞间封有一定质量空气,气柱长L=20cm,活塞A上方的水银高为H=15cm,两活塞的重力及活塞与筒壁间的摩擦不计.用外力向上托住活塞B使之处于平衡状态,水银面与粗筒上端相平.现使活塞B缓慢上移,直至水银的$\frac{1}{3}$被推入细筒中,求活塞B上移的距离.设整个过程中气柱的温度不变,大气压P0相当于75cm水银柱产生的压强.
如图,竖直圆筒固定不动,粗筒的横截面积是细筒的3倍,细筒足够长.粗筒中A,B两轻质活塞间封有一定质量空气,气柱长L=20cm,活塞A上方的水银高为H=15cm,两活塞的重力及活塞与筒壁间的摩擦不计.用外力向上托住活塞B使之处于平衡状态,水银面与粗筒上端相平.现使活塞B缓慢上移,直至水银的$\frac{1}{3}$被推入细筒中,求活塞B上移的距离.设整个过程中气柱的温度不变,大气压P0相当于75cm水银柱产生的压强. 在用如图装置“验证力的平行四边形定则”实验时:
在用如图装置“验证力的平行四边形定则”实验时: