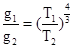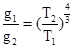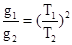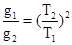题目内容
使物体脱离某星球的引力束缚，不再绕星球运行，从星球表面发射所需的最小速度称为第二宇宙速度，星球的第二宇宙速度v2与第一宇宙速度v1的关系是
1。已知某星球的半径为r，它表面的重力加速度为地球表面重力加速度g的
。不计其他星球的影响，则该星球的第二宇宙速度为
A． | B． | C． | D． |
B
解析试题分析：第一宇宙速度是最大的环绕速度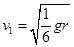
，所以第二宇宙速度为
，B正确，A.C.D错误。
考点：本题考查了第一宇宙速度和第二宇宙速度的计算
某星球与地球的质量比为a，半径比为b，则该行星表面的重力加速度与地球表面重力加速度之比为
| A．a/b | B．a/b2 | C．ab2 | D．ab |
四名同学关于人造卫星所需向心力的问题发生了争论，请对下面同学的观点进行判断，正确的是（ ）
A．张糊涂认为，当人造地球卫星的半径增大到原来的3倍时， 向心力也增大到原来的3倍，因为 |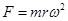
B．张模糊认为，当人造地球卫星的半径增大到原来的3倍时， 向心力减小到原来的 ，因为 |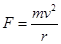
C．张清楚认为，当人造地球卫星的半径增大到原来的3倍时， 向心力减小到原来的 ，因为 |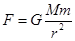
| D．张明白同学认为，仅仅知道人造卫星轨道半径的变化量，无法确定向心力的变化 |
2012年6月18日14时许，在完成捕获、缓冲、拉近和锁紧程序后，神州九号与天宫一号紧紧相连，中国首次载人交会对接取得圆满成功。神州九号飞船发射前约20天，天宫一号目标飞行器从350km轨道上开始降轨，进入高度约为343km的近圆对接轨道，建立载人环境，等待与飞船交会对接。根据以上信息，若认为它们对接前、后稳定飞行时均做匀速圆周运动，则（ ）
| A．“天宫一号”在350km轨道上飞行的速度比第一宇宙速度大 |
| B．“天宫一号”在350km轨道上飞行的动能比在343km对接轨道上小 |
| C．“天宫一号”在350km轨道上飞行的周期比在343km对接轨道上小 |
| D．“天宫一号”在350km轨道上飞行的向心加速度比在343km对接轨道上大 |
课堂上老师给同学们布置了这样一个题目：假设地球是一半径为R，质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。求矿井底部和地球表面处的重力加速度大小之比。李明同学的思考过程如下： 由等式GM=gR2（G为引力常量，M为地球质量，R为地球半径，g为地球表面处的重力加速度）变形后得到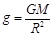
，则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比
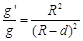。下列说法中正确的是
| A．李明的答案是正确的 |
| B．李明的答案是错误的，因为等式GM=gR2不成立 |
| C．李明的答案是错误的，因为本题不能用等式GM=gR2求解 |
| D．李明的答案是错误的，本题虽然能用等式GM=gR2求解，但他分析问题时出现错误 |
我国“二炮”的一系列导弹，在“北斗”定位系统的引导下，能实现精确打击移动目标和固定目标。假设从地面上A点发射一枚远程弹道导弹，仅在地球引力作用下，沿ACB椭圆轨道飞行击中地面目标B， C为轨道的远地点，距地面高度为h，若ACB轨迹长恰好为整个椭圆的一半。已知地球半径为R，地球质量为M，引力常量为G。则下列结论正确的是 （ ）
A．导弹在C点的速度大于  |
| B．地球的球心位于导弹椭圆轨道的一个焦点上 |
C．导弹在C点的加速度等于 |
| D．导弹从A点到B点的飞行时间等于导弹飞行周期的一半 |
设地球赤道上随地球自转的物体线速度为v1，周期为T1；近地卫星线速度为v2，周期为T2；地球同步卫星线速度为v3，周期为T3；月球绕地球运转的线速度为v4，周期为T4。则下列判断正确的是（ ）
| A．v1＝v2 | B．T1＝T3 |
| C．v1＜v2＜v3＜v4 | D．v1＞v2＞v3＞v4 |
甲、乙为两颗地球卫星，其中甲为地球同步卫星，乙的运行高度低于甲的运行高度，两卫星轨道均可视为圆轨道．以下判断正确的是
| A．甲的周期大于乙的周期 |
| B．乙的速度大于第一宇宙速度 |
| C．甲的加速度小于乙的加速度 |
| D．甲在运行时能经过北极的正上方 |