题目内容
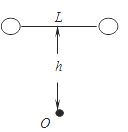
【题目】如图,两个相同的带电小球A和B,用长度为L的轻质绝缘细杆相连,A和B质量均为 m,带电量均为 +q.现将AB由竖直位置从静止开始释放,释放时B离虚线的高度为H,虚线所在水平面的下方有电场强度大小为E、方向竖直向上的电场,且
![]() (重力加速度为g).
(重力加速度为g).
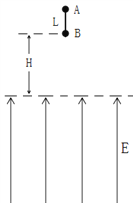
(1)求B球刚进入电场时的速度v;
(2)从释放到A刚好进入电场所经过的时间T;
(3)从A进入电场之后的![]() 时间里,AB的运动情况(包括速度、加速度的变化情况).
时间里,AB的运动情况(包括速度、加速度的变化情况).
【答案】(1) ![]() (2)
(2) 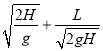 (3) 在0~
(3) 在0~ ![]() 时间内,做加速度为g的匀减速直线运动,速度从
时间内,做加速度为g的匀减速直线运动,速度从![]() 变为0 在
变为0 在![]() ~2
~2![]() 时间内,向上做加速度大小为g的匀加速运直线动,速度从0变为
时间内,向上做加速度大小为g的匀加速运直线动,速度从0变为![]() 。
。
【解析】试题分析:根据动能定理即可求出B球刚进入电场时的速度;从释放到A刚好进入电场所经过的时间包括自由落体运动时间和匀速运动时间;根据牛顿第二定律分别求出A球进场后的不同加速度,结合运动学公式即可解题。
(1)AB做自由落体运动,根据动能定理: ![]()
解得: ![]()
(2)AB做自由落体运动在竖直方向: ![]()
解得时间为: ![]()
进入电场后受到向上的电场力等于重力mg,受力平衡做匀速直线运动有: ![]()
解得运动的时间为: ![]()
所以运动的总时间为: 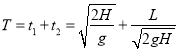
(3)当A球进入电场后,根据牛顿第二定律可得: ![]()
解得: ![]() 方向向上
方向向上
根据速度时间公式可得减速运动时间为: ![]()
所以:在0~ ![]() 时间内,做加速度为g的匀减速直线运动,速度从
时间内,做加速度为g的匀减速直线运动,速度从![]() 变为0。
变为0。
接下来A、B一起开始上上运动,根据牛顿第二定律可得: ![]()
解得: ![]() 方向向上,
方向向上,
可得![]() 时的速度为:
时的速度为: 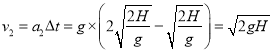
在![]() ~2
~2![]() 时间内,向上做加速度大小为g的匀加速运直线动,速度从0变为
时间内,向上做加速度大小为g的匀加速运直线动,速度从0变为![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目