��Ŀ����
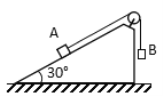
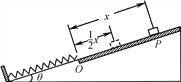
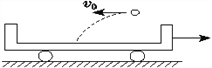
����Ŀ����ͼ����������Ϊm��С��ͨ����ΪL�IJ����쳤����ˮƽ��������h�ߴ��������䣬���������������ˮƽ��ֱ״̬��������ʱ���е�����ˮƽ���õĹ⻬����O���������ٶ�Ϊg����
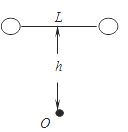
A. С��ӿ�ʼ���䵽�յ�����͵�Ĺ����л�е�ܲ��غ�
B. �������붤��������С��յ�����͵�����У������Ĺ����ȼ�С������
C. С��յ�����͵�ʱ�ٶȴ�СΪ![]()
D. С��յ�����͵�ʱ��������Ϊ![]()
���𰸡�D
��������С��ӿ�ʼ���䵽�յ�����͵�Ĺ�����ֻ��������������е���غ㣬��A����������Ϊ��������ֱ�������ΪF=mg-Tsin������ʼʱ����С��mg��Tsin����F��0����ֱ������ٶ����£�vy������Ҫ����ʱ��Tsin����mg��F��0����ֱ������ٶ����ϣ�vy��С������PG=mgvy��֪������˲ʱ������������С����B������ߵ㵽С��յ�����͵�Ĺ��������ö��ܶ����ã� ![]() mv2=mg��
mv2=mg��![]() +h������ã�v=
+h������ã�v=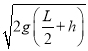 ����C���������ļ��ٶȹ�ʽ�У�
����C���������ļ��ٶȹ�ʽ�У� ![]() ������ţ�ٵڶ����ɵ�F-mg=ma�����F=
������ţ�ٵڶ����ɵ�F-mg=ma�����F=![]() +3mg����D��ȷ����ѡD��
+3mg����D��ȷ����ѡD��

��ϰ��ϵ�д�
 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
�����Ŀ