题目内容
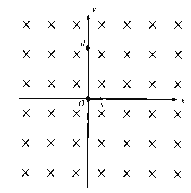
【题目】如图所示，一足够大的光滑绝缘水平桌面上建一直角坐标系xOy，空间存在垂直桌面向下的匀强磁场。一带电小球A（可视为质点）从坐标原点O以速度v沿着x轴正方向入射，沿某一轨迹运动，从（0，d）坐标向左离开第I象限。若球A在第I象限的运动过程中与一个静止、不带电的小球B（可视为质点）发生弹性正碰，碰后两球电量均分，球B的速度是球A的3倍。若不论球B初始置于何处，球A碰后仍沿原轨迹运动。球A、B的质量之比为3：1，不计两球之间的库仑力。
（1）判断带电小球A的电性并求出碰后球B的速度大小；
（2）若两球碰后恰好在（
，
）坐标首次相遇，求球B在第I象限初始位置的坐标；
（3）若将球B置于（，）坐标处，球A、B碰后，在球B离开第I象限时撤去磁场，再过时间Δt恢复原磁场，要使得两球此后的运动轨迹没有交点，求Δt的最小值。
【答案】（1）球A带正电荷 
（2）
（3）
【解析】（1）球A带正电荷
碰撞前后球A运动半径
保持不变
qvB=m1
碰后球A速度v1=
v
v2=3v1=
v
（2）由
解得
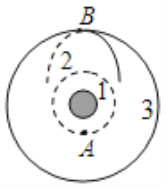
如图1所示，设两球从碰撞位置运动到（－
，）半径所夹圆心角是α，球B比球A多转2π，两球角速度之比1:3，α+2π=3α
解得α=π，所以球B被碰时在第一象限的位置为（，）
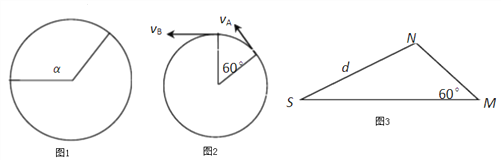
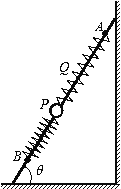
（3）如图2所示，球B离开第一象限时，两球运动轨迹半径所夹圆心角是60°。磁场消失后，各自沿着图中速度方向做匀速直线运动，当磁场恢复后，两球又做匀速圆周运动，且半径相等都是。
撤去磁场时，两球运动轨迹的圆心位置均为图3中的M点，恢复磁场，当两球的圆形运动轨迹恰好相切时，△t为最小，此时球A、B的圆心位置分别为N、S。
=1:3， 
；
见图3，根据余弦定理可得：△t=
练习册系列答案
相关题目
