题目内容
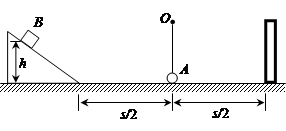
(14分)如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,其质量为m、电荷量为+q(可视为点电荷,不影响电场的分布.),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时速度为v,已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求: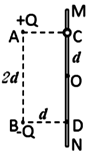
(1)C、O间的电势差UCO;
(2)小球p在O点时的加速度;
(3)小球p经过与点电荷B等高的D点时的速度大小.
(1) (2)
(2)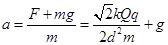 (3)
(3)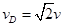
解析试题分析:(1)小球p由C运动到O时,由动能定理,
得: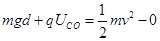 (+3分)
(+3分)
∴ (+1分)
(+1分)
(2) 小球p经过O点时受力如图: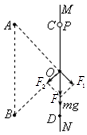
由库仑定律得: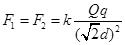 (+1分)
(+1分)
它们的合力为: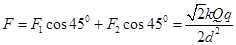 (+1分)
(+1分)
∴p在O点处的加速度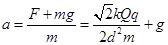 (+2分)
(+2分)
方向竖直向下 (+1分)
(3)由电场特点可知,在C、D间电场的分布是对称的
即小球p由C运动到O与由O运动到D的过程中合外力做的功是相等的, (+2分)
运用动能定理 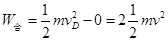 (+2分)
(+2分)
解得 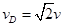 (+1分)
(+1分)
考点:小球下落过程中加速度变化,求解电势差利用动能定理;求解在O点的加速度,关键求出两点电荷在O点产生的电场力,再结合牛顿第二定律解答;由于是等量异种电荷产生的电场,O点在其连线的中垂线上,且CD关于O点对称,所以CO与OD的电势差大小相等,再结合动能定理求解即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
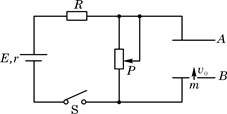
 ,sin370=0.6,cos370=0.8。
,sin370=0.6,cos370=0.8。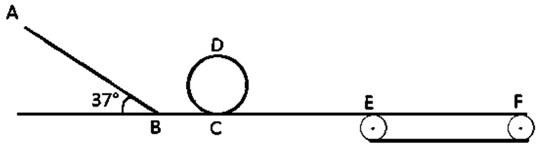
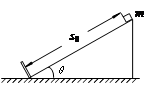
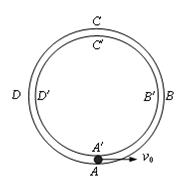

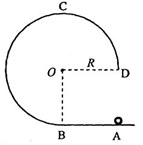
 圆弧形光滑细圆管轨道ABC,放置在竖直平面内.轨道半径为R,在A点与水半地面AD相接,地面与圆心O等高,MN是放在水平地面上长为3R,厚度不计的垫子,左端M正好位于A点将一个质量为m、直径略小于圆管直径的小球从A处管口正上方某处由静止释放,不考虑空气阻力。
圆弧形光滑细圆管轨道ABC,放置在竖直平面内.轨道半径为R,在A点与水半地面AD相接,地面与圆心O等高,MN是放在水平地面上长为3R,厚度不计的垫子,左端M正好位于A点将一个质量为m、直径略小于圆管直径的小球从A处管口正上方某处由静止释放,不考虑空气阻力。