题目内容
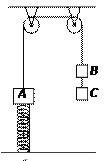
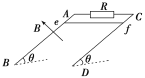
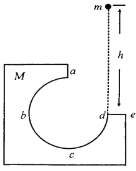
【题目】如图所示,M为固定在桌面上的木块,M上有一个![]() 圆弧的光滑轨道abcd,a为最高点,bd为其水平直径,de面水平且有足够的长度,将质量为m的小球在d点的正上方高h处从静止释放,让它自由下落到d点切入轨道内运动,则
圆弧的光滑轨道abcd,a为最高点,bd为其水平直径,de面水平且有足够的长度,将质量为m的小球在d点的正上方高h处从静止释放,让它自由下落到d点切入轨道内运动,则
A. 在h为一定值的情况下,释放后,小球的运动情况与其质量的大小无关
B. 只要改变h的大小,就能使小球通过a点后,既可以使小球落到轨道内,也可以使小球落到de面上
C. 无论怎样改变h的大小,都不能使小球通过a点后又落回到轨道内
D. 使小球通过a点后飞出de面之外(e的右边)是可以通过改变h的大小来实现的
【答案】ACD
【解析】
据牛顿第二定律分析小球的加速度与质量的关系.若小球恰能通过a点,其条件是小球的重力提供向心力,根据牛顿第二定律可解得小球此时的速度,用平抛运动的规律:水平方向的匀速直线运动,竖直方向的自由落体运动规律求出水平距离,由机械能守恒定律可求得h,分析小球能否通过a点后落回轨道内.
若小球能通过a点,则由mg(hR)=![]() mva2,可得va=
mva2,可得va=![]() ,小球的运动情况与其质量的大小无关。故A正确;由mg=m
,小球的运动情况与其质量的大小无关。故A正确;由mg=m![]() ,可得vmin=
,可得vmin=![]() ,由此求得最小水平射程
,由此求得最小水平射程![]() ,大于R,故无论怎样改变h的大小,都不能使小球通过a点后又落回到轨道内,故B错误,C正确;h越大,va越大,水平射程越大,故增大h,可使小球通过a点后飞出de面之外,故D正确。故选ACD。
,大于R,故无论怎样改变h的大小,都不能使小球通过a点后又落回到轨道内,故B错误,C正确;h越大,va越大,水平射程越大,故增大h,可使小球通过a点后飞出de面之外,故D正确。故选ACD。

【题目】(1)在做“用单摆测定重力加速度”的实验中,某同学甲用毫米刻度尺测得摆线长![]() ;用游标卡尺测得摆球的直径如图所示,则摆球直径
;用游标卡尺测得摆球的直径如图所示,则摆球直径![]() ____________
____________![]() .
.
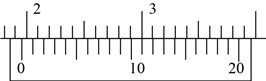
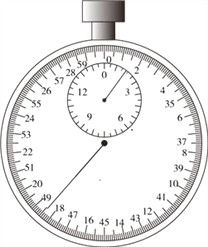
用秒表测得单摆完成![]() 次全振动的时间如图所示,则秒表的示数
次全振动的时间如图所示,则秒表的示数![]() ____________
____________![]() ;若用给出的各物理量符号(L0、
;若用给出的各物理量符号(L0、![]() 、
、![]() 、
、![]() )表示当地的重力加速度
)表示当地的重力加速度![]() ,则计算
,则计算![]() 的表达式为
的表达式为![]() ____________.
____________.
(2)实验中同学甲发现测得的![]() 值偏小,可能的原因是_______
值偏小,可能的原因是_______
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表过迟按下
D.实验中误将![]() 次全振动计为
次全振动计为![]() 次
次
(3)为了提高实验精度,某同学乙在实验中通过改变几次摆长![]() ,并测出相应的周期
,并测出相应的周期![]() ,从而得到一组对应的
,从而得到一组对应的![]() 与
与![]() 的数据,再以
的数据,再以![]() 为横坐标、
为横坐标、![]() 为纵坐标,建立坐标系,将所得数据进行连线,实验测得的数据如下表所示:
为纵坐标,建立坐标系,将所得数据进行连线,实验测得的数据如下表所示:
次数 |
|
|
|
|
|
摆长 |
|
|
|
|
|
|
|
|
|
|
|
振动周期 |
|
|
|
|
|
振动周期的平方 |
|
|
|
|
|
请将表中第三次测量数据标在右图中,并在右图中作出![]() 随
随![]() 变化的关系图象__________.
变化的关系图象__________.
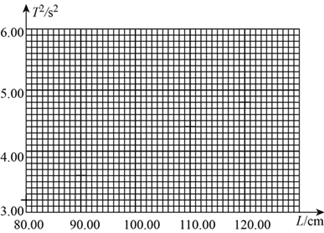
②根据图象,可知当地的重力加速度为____________(保留![]() 位有效数字).
位有效数字).