题目内容
【题目】如图所示,两根足够长的光滑平行直导轨AB、CD与水平面成θ角放置,两导轨间距为L,A、C两点间接有阻值为R的定值电阻。一根质量为m、长也为L的均匀直金属杆ef放在两导轨上,并与导轨垂直。整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直于导轨平面向上,导轨和金属杆接触良好,金属杆ef的电阻为r,其余部分电阻不计。现让ef杆由静止开始沿导轨下滑。
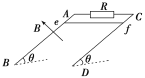
(1)求ef杆下滑的最大速度vm。
(2)已知ef杆由静止释放至达到最大速度的过程中,ef杆沿导轨下滑的距离为x,求此过程中定值电阻R产生的焦耳热Q和在该过程中通过定值电阻R的电荷量q。
【答案】(1)![]()
(2)![]()
![]()
【解析】
试题分析:(1)对ef杆,由牛顿第二定律有
mgsinθ-BIL=ma
又![]() ,所以有
,所以有
![]()
当加速度a为零时,速度v达到最大,速度最大值![]()
(2)根据能量守恒定律有
mgxsinθ=![]() mvm2+Q总
mvm2+Q总
由公式Q=I2Rt,可得![]()
又QR+Qr=Q总
解得![]()
由法拉第电磁感应定律有![]()
又由闭合电路的欧姆定律有![]()
解得![]() 。
。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目