��Ŀ����
����Ŀ����ͼ����һ����ΪM=2kg��ƽ�峵��ֹ�ڹ⻬��ˮƽ�����ϣ�����������Ϊm=1kg��С���A��B��������Ϊ�ʵ㣩���ɳ���P����ʼ��A�Գ��ٶ�v1=2m/s�����˶���Bͬʱ��v2=4m/s�����˶�������A��B�����ǡ��ͣ��С������û������С�����������С����Ķ�Ħ��������Ϊ��=0.1��ȡg=10m/s2 �� ��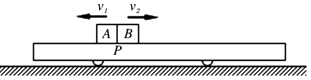
��1����С���ܳ���
��2����ʼʱB��С���Ҷ˵ľ��룻
��3����A��B��ʼ�˶���ʱ����6sС����ԭλ�õľ���x��
���𰸡�
��1���⣺�����ﵽ��ͬ�ٶ�v������ϵͳ�����غ㣬ѡȡ����Ϊ�����������غ㣬�У�
mv2��mv1=��2m+M��v
![]()
�������ݽ�ã�v=0.5m/s��L=9.5m
��С���ܳ�Ϊ9.5m��
��2���⣺A������˾���x1���˶��������ʱt1����A�˶������ǰ��ľ�徲ֹ����mg=maA��v1=aAt1�� ![]() ��
��
��ã�t1=2s��x1=2m
B���Ҷ˾���Ϊ��x2=L��x1=7.5m
�𣺿�ʼʱB��С���Ҷ˵ľ���Ϊ7.5m��
��3���⣺����鿪ʼ���ﹲ����ʱt2���У�v=v2��aBt2��
�֣���mg=maB��
��ã�t2=3.5s
С����t1ǰ��ֹ����t1��t2֮����a���Ҽ��٣���С����A��ɵ�ϵͳΪ�о�������ţ�ٵڶ����ɵã���mg=��M+m��a
С��������λ��Ϊ�� ![]()
����������������ɵ�ϵͳ��v��ͬ�����˶���s'=v��6s��t2��
С����6s�������ߵ��ܾ���Ϊ��x=s+s'
�������ݵã�x=1.625m
�𣺴�A��B��ʼ�˶���ʱ����6sС����ԭλ�õľ�����1.625m��
����������1�����ڿ�ʼʱ���A��B��С����Ħ������С��ȣ������෴��С�����������A��B�������˶������ٶ�a��Сһ����A���ٶ��ȼ�Ϊ�㣻A��С���ϻ��������У�BҲ���ȼ����˶���A���ٶȼ�СΪ0��B������С���ϼ��ٻ�������С����Aһ�����ҷ�����٣������⻬���������A��B��С����ɵ�ϵͳ�����غ㣬���ݶ����غ㶨�������ͬ�ٶȣ����ݹ��ܹ�ϵ��ʽ����˹�����B�˶���λ�ƣ�����λ��֮�ͼ�ΪС���ij��ȣ���2��A��С���ϻ����Ĺ����в�������������A���������п˷�Ħ�������Ĺ����ɹ��ܹ�ϵ���������ʼʱA��С����˵ľ��룬Ȼ���ɼ��ι�ϵ�����������3��С����A��Ħ�����������������˶�����ţ���˶����ɿɵ�С���˶��ļ��ٶȣ��ٸ����˶�ѧ������ʽ������⣮
�����㾫����������Ŀ����֪���������ö����غ㶨�ɺ������غ㶨�ɵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣻�����غ㶨�ɣ������Ȳ�������Ҳ���ᴴ������ֻ���һ����ʽת��Ϊ������ʽ�����ߴ�һ������ת�Ƶ���һ�����壬����ת����ת�ƹ����У��������������ֲ��䣮

 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�