题目内容
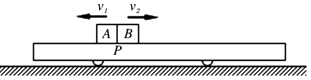
【题目】如图所示,质量M=4kg的L型木板AB静止放在光滑的水平面上,木板右端D点固定着一根轻质弹簧,C点时弹簧的自由端,CD段木板时光滑的,其他部分是粗糙的.质量m=1kg的小木块(可视为质点)静止在木板的左端,与木板间的动摩擦因数μ=0.2.现对木板AB施加水平向左F=14N的恒力,当作用1s后撤去F,这时小木块也刚好到达弹簧的自由端C点,取g=10m/s2 . 则:
(1)弹簧的自由端C点到木板左端的距离为多少?
(2)小木块在压缩弹簧的过程中,弹簧获得的最大弹性势能EP0为多少?
【答案】
(1)解:根据牛顿第二定律得物块的加速度为:
![]() ,
,
木板的加速度为:
![]() ,
,
则弹簧的自由端C到木板左端的距离为:
![]() =
= ![]() .
.
答:弹簧的自由端C点到木板左端的距离为0.5m.
(2)解:撤去F时,物块的速度为:
v1=a1t=2×1m/s=2m/s
木板的速度为:
v2=a2t=3×1m/s=3m/s,
规定向左为正方向,根据动量守恒得:
mv1+Mv2=(m+M)v,
解得:v= ![]() ,
,
则弹簧获得的最大弹性势能为:
![]() ,
,
代入数据解得:Ep0=0.4J.
答:小木块在压缩弹簧的过程中,弹簧获得的最大弹性势能EP0为0.4J.
【解析】(1)根据牛顿第二定律分别求出木块和木板的加速度,结合位移时间公式求出弹簧的自由端C点到木板左端的距离.(2)当木块和木板速度相等时,弹簧的弹性势能最大,根据动量守恒定律求出共同速度,结合能量守恒求出最大的弹性势能.
【考点精析】关于本题考查的弹性势能和动量守恒定律,需要了解弹性势能是物体由于发生弹性形变而具有的能量;动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变才能得出正确答案.

 阅读快车系列答案
阅读快车系列答案