题目内容
【题目】一质量为![]() ,倾角为
,倾角为![]() 的斜面放置在光滑水平面上,另一质量为
的斜面放置在光滑水平面上,另一质量为![]() 、半径为
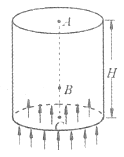
、半径为![]() 的均匀圆柱体沿斜面无滑动滚下,如图所示
的均匀圆柱体沿斜面无滑动滚下,如图所示

(1)建立斜面和圆柱体的动力学方程,并指出圆柱体作纯滚动的运动学条件
(2)确定此力学系统的守匣量,并给出具体的表达式
(3)求解斜面的加速度,以及圆柱体质心相对于斜面的加速度
【答案】(1) 即![]() ,圆柱体作纯滚动的条件为
,圆柱体作纯滚动的条件为![]() (2)
(2) ![]() (3) 解得斜面加速度和圆柱体质心
(3) 解得斜面加速度和圆柱体质心![]() 的相对加速度分别为
的相对加速度分别为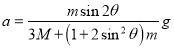 ,
,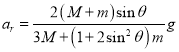
【解析】
选择地面为定参考系,动参考系![]() 在斜面上,如图所示.设斜面有向右的加速度
在斜面上,如图所示.设斜面有向右的加速度![]() ,圆柱体质心
,圆柱体质心![]() 有相对于斜面的加速度
有相对于斜面的加速度![]() (设其方向沿斜面向下),以圆柱体质心
(设其方向沿斜面向下),以圆柱体质心![]() 为动点,斜面为动系,由加速度合成定理
为动点,斜面为动系,由加速度合成定理![]() ,而
,而![]() ,故有
,故有![]() .于是,得到
.于是,得到![]() ,
,![]() .
.
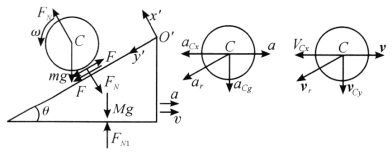
对斜面应用质心运动定理,有
![]() . ①
. ①
对圆柱体质点,其运动微分方程为
![]() ,
,
![]() .
.
考虑到![]() ,
,![]() .于是,有
.于是,有
![]() , ②
, ②
![]() . ③
. ③
设圆柱体转动的角加速度为![]() (设
(设![]() 为逆时针转,根据动量矩定理,有
为逆时针转,根据动量矩定理,有
![]() ,即
,即![]() . ④
. ④
圆柱体作纯滚动的条件为![]() . ⑤
. ⑤
(2)设斜面有向右的速度![]() ,圆柱体质心
,圆柱体质心![]() 相对于斜面有向下的速度
相对于斜面有向下的速度![]() ,如图所示,根据速度合成定理,有
,如图所示,根据速度合成定理,有![]() ,而
,而![]() ,故有
,故有![]() .于是,得到
.于是,得到![]() ,
,![]() .
.
以斜面和圆柱体组成系统,该系统水平方向上不受外力,由系统水平方向上动量守恒,可得
![]() .
.
两边对时间![]() 求导,并考虑到
求导,并考虑到![]() ,
,![]() ,即得
,即得
![]() . ⑥
. ⑥
(3)联立式①~⑥,解得斜面加速度和圆柱体质心![]() 的相对加速度分别为
的相对加速度分别为
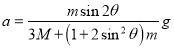 ,
,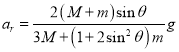

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目