��Ŀ����
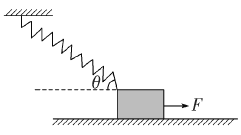
����Ŀ�������ַ綴����һ��Ƽ��뾪�����ϵ�������Ŀ��������һ���ض��Ŀռ��ڰѱ����ߡ���������������綴�����ϵķ����ͷ��ٱ��ֲ��䣬�����ߵ����������̬��ͨ���ı��ܷ�������������ڴ�ֱ���������ͶӰ����������ı��������Ϸ����Ĵ�С����֪�������ܷ�����С���ܷ���������ȣ���ˮƽ����ʱ�ܷ���������ΪS0��վ��ʱ�ܷ����Ϊ![]() �����ܷ����Ϊ
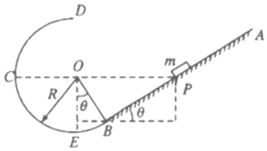
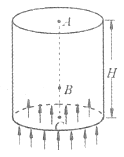
�����ܷ����Ϊ![]() ʱ��������ǡ�ÿ��Ծ�ֹ������Ư�ơ���ͼ��ʾ��ij�α����У�����������ƶ��Ŀռ��ܸ߶�ΪH���������ɾ�ֹ��վ�����˴�Aλ�����䣬����Bλ��ʱ����Ϊˮƽ�������ˣ����Ƶ������̵�ʱ����ٶȱ仯�����˶���Cλ���ٶ�ǡ�ü�Ϊ�㡣���ڱ���������Ĺ��̣�����˵������ȷ����
ʱ��������ǡ�ÿ��Ծ�ֹ������Ư�ơ���ͼ��ʾ��ij�α����У�����������ƶ��Ŀռ��ܸ߶�ΪH���������ɾ�ֹ��վ�����˴�Aλ�����䣬����Bλ��ʱ����Ϊˮƽ�������ˣ����Ƶ������̵�ʱ����ٶȱ仯�����˶���Cλ���ٶ�ǡ�ü�Ϊ�㡣���ڱ���������Ĺ��̣�����˵������ȷ����
A. ��A��B���̱����ߵļ��ٶȴ��ڴ�B��C���̱����ߵļ��ٶ�
B. ��A��B���̱����ߵ��˶�ʱ����ڴ�B��C���̱����ߵ��˶�ʱ��
C. ��A��B���̱����߶��ܵı仯�����ڴ�B��C���̱����߿˷����������Ĺ�
D. ��A��B���̱����߶����仯������ֵС�ڴ�B��C���̱������ܷ�����������ֵ
���𰸡�BD
��������
����ˮƽ����ʱ�ܵ��ķ�����СΪFm�����������ܷ�����С��������������ȣ�����վ��ʱ����Ϊ![]() Fm�������ܷ�����Ч��������ֵ��һ��ʱ��ǡ�ÿ��Ծ�ֹ������Ư�ƣ��ʿ�������˵����� G=
Fm�������ܷ�����Ч��������ֵ��һ��ʱ��ǡ�ÿ��Ծ�ֹ������Ư�ƣ��ʿ�������˵����� G=![]() Fm������ Fm=2G�����A��B���̱����ߵļ��ٶ�Ϊ
Fm������ Fm=2G�����A��B���̱����ߵļ��ٶ�Ϊ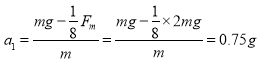 ;��B��C���̱����ߵļ��ٶȴ�СΪ a2=
;��B��C���̱����ߵļ��ٶȴ�СΪ a2=![]() =g����˴�A��B���̱����ߵļ��ٶ�С�ڴ�B��C���̱����ߵļ��ٶȡ���A������B����ٶ�Ϊv�����A��B���̱����ߵ��˶�ʱ��
=g����˴�A��B���̱����ߵļ��ٶ�С�ڴ�B��C���̱����ߵļ��ٶȡ���A������B����ٶ�Ϊv�����A��B���̱����ߵ��˶�ʱ��![]() ����B��C���̱����ߵ��˶�ʱ��
����B��C���̱����ߵ��˶�ʱ��![]() ����t1��t2����B��ȷ�����ٶ�λ�ƹ�ʽ�ã���A��B���̱����ߵ�λ�� x1=
����t1��t2����B��ȷ�����ٶ�λ�ƹ�ʽ�ã���A��B���̱����ߵ�λ�� x1=![]() ����B��C���̱����ߵ�λ�� x2=
����B��C���̱����ߵ�λ�� x2=![]() ����x1��x2=a2��a1=4��3������� x1=
����x1��x2=a2��a1=4��3������� x1=![]() H����A��B����Ӧ�ö��ܶ�����������A��B���ܵ�������Ek=��mg-
H����A��B����Ӧ�ö��ܶ�����������A��B���ܵ�������Ek=��mg-![]() Fm��
Fm��![]() H=
H=![]() FmH��B��C�˷��������Ĺ� W2=Fm
FmH��B��C�˷��������Ĺ� W2=Fm![]() H=
H=![]() FmH����֪����Ek=W2����������A��B���ܵ���������B��C�˷��������Ĺ�����C�����ݶ��������ã���A��B���̱����߶����仯����p1=��mg-
FmH����֪����Ek=W2����������A��B���ܵ���������B��C�˷��������Ĺ�����C�����ݶ��������ã���A��B���̱����߶����仯����p1=��mg-![]() Fm��t1=��
Fm��t1=��![]() Fm-
Fm-![]() Fm��
Fm��![]() =
=![]() ����B��C���̱������ܷ�����������ֵ I2=Fmt2=
����B��C���̱������ܷ�����������ֵ I2=Fmt2=![]() ������p1��I2������A��B���̱����߶����仯������ֵС�ڴ�B��C���̱������ܷ�����������ֵ����D��ȷ����ѡBD��
������p1��I2������A��B���̱����߶����仯������ֵС�ڴ�B��C���̱������ܷ�����������ֵ����D��ȷ����ѡBD��

 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�