Question

【题目】如图所示,位于竖直平面上的1/4圆弧光滑轨道，半径为R，OB沿竖直方向，圆弧轨道上端A点距地面高度为H，质量为m的小球从A点静止释放，到B点的速度为，最后落在地面C点处，不计空气阻力。试求：

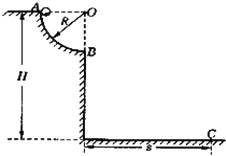
（1）小球刚运动到B点时，对轨道的压力多大?

（2）小球落地点C与B的水平距离S为多少?

（3）比值R/H为多少时，小球落地点C与B水平距离S最远?该水平距离的最大值是多少?

Answer 1

【答案】（1）3mg（2）（3）当时，s最大值

【解析】

试题分析：（1）小球沿圆弧做圆周运动，在B点由牛顿第二定律

有

解得NB=3mg

根据牛顿第三定律，小球对轨道的压力大小等于轨道对小球的支持力，为3mg

（2）小球由B→C过程，

水平方向有：s=vB·t

竖直方向有：

解得

（3）水平距离：

所以，当时，s最大．