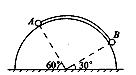
题目内容
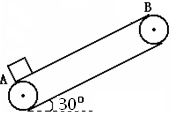
(8分)如图所示,传送带与地面成夹角θ=30°,以5m/s的速度顺时针转动,在传送带下端A处轻轻地放一个质量m=2㎏的物体,它与传送带间的动摩擦因数μ=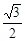 ,已知传送带从A到传送带顶端B的长度L=15m,物体从A运动到B的过程中,
,已知传送带从A到传送带顶端B的长度L=15m,物体从A运动到B的过程中,
(1)所需要的时间为多少?
(2)传送带对物体所做的功是多少?
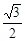 ,已知传送带从A到传送带顶端B的长度L=15m,物体从A运动到B的过程中,
,已知传送带从A到传送带顶端B的长度L=15m,物体从A运动到B的过程中,
(1)所需要的时间为多少?
(2)传送带对物体所做的功是多少?
(1)t= t1+ t2=" 4" s(2)175 J
(1)物体加速过程中,有
得: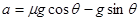 ="2.5" m/s2
="2.5" m/s2
此过程 t1=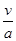 ="2" s
="2" s
x1= ="5" m
="5" m
因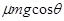 >
> ,共速之后匀速上升 t2=
,共速之后匀速上升 t2=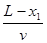 ="2" s
="2" s
物体从A运动到B的过程所需要的时间t= t1+ t2=" 4" s
(2) 物体加速过程中,滑动摩擦力做功W1=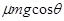 ·x1="75" J
·x1="75" J
物体匀速过程中,静摩擦力做功W2=f·(L- x1)= ·(L- x1)="100" J
·(L- x1)="100" J
传送带对物体所做的功W= W1+ W2=" 175" J
本题考查对牛顿第二定律的应用,在加速过程中由重力沿斜面向下的分力和摩擦力提供加速度,求得加速度后再由运动学公式求解,在第二问中考查对动能定理的应用,选定研究过程,利用动能定理列公式求解

得:
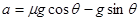 ="2.5" m/s2
="2.5" m/s2此过程 t1=
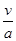 ="2" s
="2" s x1=
 ="5" m
="5" m因
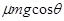 >
> ,共速之后匀速上升 t2=
,共速之后匀速上升 t2=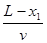 ="2" s
="2" s物体从A运动到B的过程所需要的时间t= t1+ t2=" 4" s
(2) 物体加速过程中,滑动摩擦力做功W1=
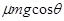 ·x1="75" J
·x1="75" J物体匀速过程中,静摩擦力做功W2=f·(L- x1)=
 ·(L- x1)="100" J
·(L- x1)="100" J传送带对物体所做的功W= W1+ W2=" 175" J
本题考查对牛顿第二定律的应用,在加速过程中由重力沿斜面向下的分力和摩擦力提供加速度,求得加速度后再由运动学公式求解,在第二问中考查对动能定理的应用,选定研究过程,利用动能定理列公式求解

练习册系列答案
相关题目
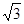
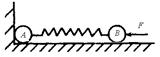


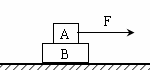
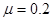 ,A物上系一细线,细线能承受的最大拉力是20N,水平向右拉细线,若最大静摩擦力约为滑动摩擦力,下述中正确的是(g=10m/s2)( )
,A物上系一细线,细线能承受的最大拉力是20N,水平向右拉细线,若最大静摩擦力约为滑动摩擦力,下述中正确的是(g=10m/s2)( )