题目内容
【题目】（10分）动车组列车（如图17所示）是由几节自带动力的车厢（动车）加几节不带动力的车厢（拖车）编成一组，它将动力装置分散安装在多节车厢上。在某次试运行中共有4节动车和4节拖车组成动车组，每节动车可以提供Pe=750kW的额定功率，每节车厢平均质量为m=20t。该次试运行开始时动车组先以恒定加速度a=0.5m/s2启动做直线运动，达到额定功率后再做变加速直线运动，总共经过550s的时间加速后，动车组便开始以最大速度vm=270km/h匀速行驶。设每节动车在行驶中的功率相同，行驶过程中每节车厢所受阻力相同且恒定。求：
（1）动车组在匀加速阶段的牵引力大小；
（2）动车组在整个加速过程中每节动车的平均功率；
（3）动车组在整个加速过程中所通过的路程（计算结果保留两位有效数字）。
【答案】(1)1.2×105N (2) 715.9kW (3) 28km
【解析】
试题设动车组在运动中所受阻力为Ff ，动车组的牵引力为F，
动车组以最大速度匀速运动时，F=Ff
动车组总功率 P=Fvm=Ff vm ，P=4Pe （1分）
解得 Ff =4×104N
设动车组在匀加速阶段所提供的牵引力为F，
由牛顿第二定律有 F - Ff = 8ma （1分）
解得 F =1.2×105N （1分）
（2）设动车组在匀加速阶段所能达到的最大速度为v，匀加速运动的时间为t1，
由P=F v 解得 v=25m/s （1分）
由运动学公式 v=at1 解得t1=50s
动车在非匀加速运动的时间 t2=t-t1=500s （1分）
动车组在加速过程中每节动车的平均功率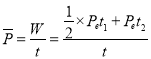 
代入数据解得 
=715.9kW（或约为716kW） （2分）
（3）设动车组在加速过程中所通过的路程为s，由动能定理
（1分）
解得 s=28km （2分）
应用题天天练四川大学出版社系列答案
