Question

【题目】高台滑雪以其惊险明激而闻名，运动员在空中的飞跃姿势具有很强的观赏性。某滑雪轨道的完整结构可以简化成如图12所示的示意图，其中AB段是助滑坡，倾角a＝，BC段是水平起跳台，CD段是着陆坡，倾角=，DE段是停止区，AB段与BC段圆滑相连，轨道各部分与滑雪板间的动摩擦因数均为，图中轨道最高点A处的起滑台距起跳台BC的竖直高度h=47m， 运动员连同滑雪板的质量m＝60kg，滑雪运动员从A点由静止开始起滑，通过起台从C点水平飞出，运动员在着陆坡CD上的着陆位置与C点的距高l=120m，设运动员在起跳前不使用雪杖助滑，忽略空气阻力的影响，取重力加速度g＝10sin37＝0．6，cos37＝0.8。求

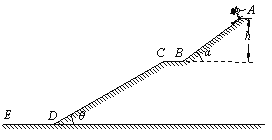
（1）运动员在助滑坡AB上运动加速度的大小

（2）运动员在C点起跳时速度的大小

（3）运动员从起滑台A点到起台C点的过程中克服摩擦力所做的功

Answer 1

【答案】（1）5.76m/s2（2）120m（3）1200J

【解析】

根据牛顿第二定律求运动员在助滑坡AB上运动时加速度；运动员从C点起跳后做平抛运动，根据运动的分解法，分别列出水平位移和竖直位移与时间的关系，由竖直位移与水平位移之比tanθ，求出时间，再求得C点到着陆坡上着陆点的距离；运动员从起滑台A点到起跳台C点的过程，运用动能定理求克服摩擦力所做的功．

（1）运动员在助滑坡AB上运动时，

根据牛顿第二定律得，

解得．
（2）设运动员从C点起跳后到落到着陆坡上的时间为t，C点到着陆坡上着陆点的距离为L．运动员从C点起跳后做平抛运动，则有，

竖直方向：①，水平方向②，由①：②得：，

解得

（3）运动员从起滑台A点到起跳台C点的过程，根据动能定理得，

解得：克服摩擦力所做的功