题目内容
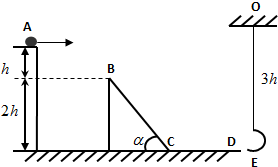 如图所示,平台上的小球从A点水平抛出,恰能无碰撞地进入光滑的BC斜面,经C点进入光滑平面CD时速率不变,最后进入悬挂在O点并与水平面等高的弧形轻质筐内.已知小球质量为m,A、B两点高度差h,BC斜面高2h,倾角α=45°,悬挂弧筐的轻绳长为3h,小球看成质点,轻质筐的重量忽略不计,弧形轻质筐的大小远小于悬线长度,重力加速度为g,试求:
如图所示,平台上的小球从A点水平抛出,恰能无碰撞地进入光滑的BC斜面,经C点进入光滑平面CD时速率不变,最后进入悬挂在O点并与水平面等高的弧形轻质筐内.已知小球质量为m,A、B两点高度差h,BC斜面高2h,倾角α=45°,悬挂弧筐的轻绳长为3h,小球看成质点,轻质筐的重量忽略不计,弧形轻质筐的大小远小于悬线长度,重力加速度为g,试求:(1)B点与抛出点A的水平距离x;
(2)小球运动至C点的速度vc大小
(3)小球进入轻质筐后瞬间,小球所受拉力F的大小.
分析:(1)小球从A到B做平抛运动,小球恰好与无碰撞地进入光滑的BC斜面,速度沿BC面向下,可得到两个方向的分速度关系.从水平方向和竖直方向运用平抛运动的规律分析解决问题.
(2)运用动能定理可求解小球到达C点的速度.
(3)小球进入轻质筐后瞬间,进行受力分析,并运用牛顿第二定律求解.
(2)运用动能定理可求解小球到达C点的速度.
(3)小球进入轻质筐后瞬间,进行受力分析,并运用牛顿第二定律求解.
解答:解:(1)小球至B点时速度方向与水平方向夹角为45°,设小球抛出的初速度为v0,A点至B点时间为t.则得:
h=
gt2,
又tan45°=
,x=v0t,
得水平距离:x=2h
(2)设小球至B点时速度为vB,在斜面上运动的加速度为a,
vB=
v0,
a=gsin45°,
由动能定理得:
-
=2a?
联立以上几式得:vC=
(3)小球进入轻筐后做圆周运动,由牛顿第二定律得:F-mg=m
,
解得小球所受拉力:F=3mg
答:
(1)B点与抛出点A的水平距离x为2h;
(2)小球运动至C点的速度vc大小为
.
(3)小球进入轻质筐后瞬间,小球所受拉力F的大小为3mg.
h=
| 1 |
| 2 |
又tan45°=
| v0 |
| gt |
得水平距离:x=2h
(2)设小球至B点时速度为vB,在斜面上运动的加速度为a,
vB=
| 2 |
a=gsin45°,
由动能定理得:
| v | 2 C |
| v | 2 B |
| 2h |
| sin45° |
联立以上几式得:vC=
| 6gh |
(3)小球进入轻筐后做圆周运动,由牛顿第二定律得:F-mg=m
| ||
| 3h |
解得小球所受拉力:F=3mg
答:
(1)B点与抛出点A的水平距离x为2h;
(2)小球运动至C点的速度vc大小为
| 6gh |
(3)小球进入轻质筐后瞬间,小球所受拉力F的大小为3mg.
点评:遇到题目过程非常复杂时,注意把题目细化分解到小的过程.比如此题中,整个过程可分为平抛、沿光滑斜面匀加速、沿水平面匀速、沿圆轨道圆周运动.

练习册系列答案
相关题目
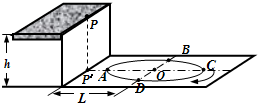 地面上有一个半径为R的圆形跑道,高为h的平台边缘上的P点在地面上P′点的正上方,P′与跑道圆心O的距离为L(L>R),如图所示.跑道上停有一辆小车,现从P点水平抛出小沙袋,使其落入小车中(沙袋所受空气阻力不计).问:
地面上有一个半径为R的圆形跑道,高为h的平台边缘上的P点在地面上P′点的正上方,P′与跑道圆心O的距离为L(L>R),如图所示.跑道上停有一辆小车,现从P点水平抛出小沙袋,使其落入小车中(沙袋所受空气阻力不计).问: 风洞实验室可产生水平方向的、大小可调节的风力.在风洞中有一个固定的支撑架ABC,该支撑架的外表面光滑,且有一半径为R的四分之一圆柱面,支撑架固定在离地面高为2R的平台上,平台竖直侧壁光滑,如图所示,地面上的D点处有一竖直的小洞,小洞离侧壁的水平距离为R,现将质量分别为m1和m2的两个小球用一根不可伸长的轻绳连接按图示的方式置于圆柱面上,球m1放在柱面底部的A点,球m2竖直下垂.
风洞实验室可产生水平方向的、大小可调节的风力.在风洞中有一个固定的支撑架ABC,该支撑架的外表面光滑,且有一半径为R的四分之一圆柱面,支撑架固定在离地面高为2R的平台上,平台竖直侧壁光滑,如图所示,地面上的D点处有一竖直的小洞,小洞离侧壁的水平距离为R,现将质量分别为m1和m2的两个小球用一根不可伸长的轻绳连接按图示的方式置于圆柱面上,球m1放在柱面底部的A点,球m2竖直下垂. (2)如图所示。在光滑的水平面上有一带有光滑平台的、质量为M=4 Kg(连同平台)的小车,平台与小车上表面的高度差为h=0.2m,在平台上用一质量为m=1Kg的小物块压缩一轻小的弹簧。开始时整个系统处于静止状态。某时刻释放小物体时弹簧将小车与物块弹开,最终物块落到与平台的右端P点的水平距离为L=0.8m的小车上表面的Q点。试求:
(2)如图所示。在光滑的水平面上有一带有光滑平台的、质量为M=4 Kg(连同平台)的小车,平台与小车上表面的高度差为h=0.2m,在平台上用一质量为m=1Kg的小物块压缩一轻小的弹簧。开始时整个系统处于静止状态。某时刻释放小物体时弹簧将小车与物块弹开,最终物块落到与平台的右端P点的水平距离为L=0.8m的小车上表面的Q点。试求:
