Question

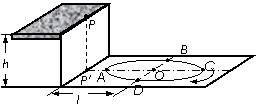
（2013福建惠安月考）地面上有一个半径为R的圆形跑道，高为h的平台边缘上的P点在地面上P′点的正上方，P′与跑道圆心O的距离为L（L>R），如图所示。跑道上停有一辆小车，现从P点水平抛出小沙袋，使其落入小车中（沙袋所受空气阻力不计）。问：

（1）当小车分别位于A点和B点时（∠AOB＝90°），沙袋被抛出时的初速度各为多大？

（2）若小车在跑道上运动，则沙袋被抛出时的初速度在什么范围内？

（3）若小车沿跑道顺时针运动，当小车恰好经过A点时，将沙袋抛出，为使沙袋能在B处落入小车中，小车的速率v应满足什么条件？

Answer 1

解析:（1）沙袋从P点被抛出后做平抛运动，设它的落地时间为t，

则           1分

当小车位于A点时，有    1分  

可得 1分

当小车位于B点时，有     1分  

可得 1分

（2）若小车在跑道上运动，要使沙袋落入小车，最小的抛出速度为

2分

若当小车经过C点时沙袋刚好落入，抛出时的初速度最大，有 1分

可得   1分

所以沙袋被抛出时的初速度范围为

 1分

（3）要使沙袋能在B处落入小车中，小车运动的时间应与沙袋下落和时间相同

（n=0，1，2，3……）  3分

   1分

得    （n=0，1，2，3……）2分