题目内容
【题目】如图所示,一质量为m的小车静止在光滑的水平面上,在它的横梁上用长为1m的细线悬挂着质量也为m的小球,开始时给小球一个水平冲量,使小球获得4m/s的水平速度向右运动.试求:(取g=10m/s2)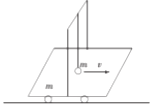
(1)小球运动到最高点时的速度.
(2)小球上升的最大高度.
(3)小球第一次回到最低点时的速度大小.
【答案】
(1)解:小球到达最高点与小车具有共同水平速度v′,系统水平动量守恒,
选向右的方向为正,有:
mv=(m+m)v′
代入数据得:v′=2m/s.
答:小球运动到最高点时的速度是2m/s.
(2)解:根据系统机械能守恒得
![]() mv2=
mv2= ![]() (m+m)v′2+mgh
(m+m)v′2+mgh
h=0.4m,
答:小球上升的最大高度是0.4m.
(3)解:根据系统水平动量守恒,选向右的方向为正,有:
mv=mv1′+mv″
根据系统机械能守恒得
![]() m
m ![]() =
= ![]() mv1′2+
mv1′2+ ![]() mv″2
mv″2
解得:mv1′=0,v″=4m/s,或mv1′=4m/s,v″=0,(舍去)
答:小球第一次回到最低点时的速度大小是0.
【解析】开始时给小球一个水平冲量,使小球获得4m/s的水平速度向右运动.小球运动过程中,系统水平方向不受外力,动量守恒,结合能量守恒求出最高点时的速度.
根据系统机械能守恒求解小球上升的最大高度.
【考点精析】解答此题的关键在于理解动量定理的相关知识,掌握动量定理的研究对象可以是单个物体,也可以是物体系统.对物体系统,只需分析系统受的外力,不必考虑系统内力.系统内力的作用不改变整个系统的总动量;动量定理不仅适用于恒定的力,也适用于随时间变化的力.对于变力,动量定理中的力F应当理解为变力在作用时间内的平均值,以及对动量守恒定律的理解,了解动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变.

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
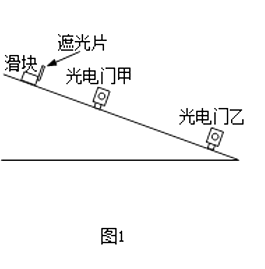
轻巧夺冠周测月考直通高考系列答案【题目】利用图1所示的装置可测量滑块在斜面上运动的加速度.一斜面上安装有两个光电门,其中光电门乙固定在斜面上靠近底端处,光电门甲的位置可移动,当一带有遮光片的滑块自斜面上滑下时,与两个光电门都相连的计时器可以显示出遮光片从光电门甲至乙所用的时间t,改变光电门甲的位置进行多次测量,每次都使滑块从同一点由静止开始下滑,并用米尺测量甲、乙之间的距离s,记下相应的t值;所得数据如表所示.完成下列填空和作图:
s(m) | 0.500 | 0.600 | 0.700 | 0.800 | 0.900 | 0.950 |
t(s) | 0.29 | 0.37 | 0.45 | 0.55 | 0.67 | 0.78 |
s/t(m/s) | 1.71 | 1.62 | 1.55 | 1.45 | 1.34 | 1.22 |
(1)若滑块所受摩擦力为一常量,滑块加速度的大小a、滑块经过光电门乙时的瞬时速度v1、测量值s和t四个物理量之间所满足的关系式是;
(2)根据表中给出的数据,在图2给出的坐标纸上画出 ![]() ﹣t图线;
﹣t图线;
(3)由所画出的 ![]() ﹣t图线,得出滑块加速度的大小为a=m/s2(保留2位有效数字).
﹣t图线,得出滑块加速度的大小为a=m/s2(保留2位有效数字).