题目内容
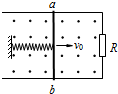
如图所示,间距为l的平行金属导轨LMN和OPQ分别固定在两个竖直面内,电阻为R、质量为m、长为l的相同导体杆ab和cd分别放置在导轨上,并与导轨垂直.在水平光滑导轨间有与水平面成θ、并垂直于ab的匀强磁场;倾斜导轨间有沿斜面向下的匀强磁场,磁感应强度均为B.倾斜导轨与水平面夹角也为θ,杆cd与倾斜导轨间动摩擦因素为μ.ab杆在水平恒力作用 下由静止开始运动,当cd刚要滑动时ab恰达到最大速度.(θ=30、μ=、最大静摩擦力等于滑动摩擦力)求:
下由静止开始运动,当cd刚要滑动时ab恰达到最大速度.(θ=30、μ=、最大静摩擦力等于滑动摩擦力)求:
(1)此时杆cd中的电流大小;
(2)杆ab的最大速度;
(3)若此过程中流过杆ab的电量为q,则cd产生的焦耳热Q为多大?
 下由静止开始运动,当cd刚要滑动时ab恰达到最大速度.(θ=30、μ=、最大静摩擦力等于滑动摩擦力)求:
下由静止开始运动,当cd刚要滑动时ab恰达到最大速度.(θ=30、μ=、最大静摩擦力等于滑动摩擦力)求:(1)此时杆cd中的电流大小;
(2)杆ab的最大速度;
(3)若此过程中流过杆ab的电量为q,则cd产生的焦耳热Q为多大?
(1)cd杆刚要滑动时,所受的静摩擦力达到最大,设最大静摩擦力为f,由平衡条件得:
mgsinθ=f
N+F安cd=mgcosθ
又有f=μN,F安cd=BIl
解得:F安cd=
mg,I=
(2)根据闭合电路欧姆定律得知:ab棒产生的感应电动势为 E=I?2R=2IR;
由法拉第电磁感应定律得:E=Blvmsinθ
解得:vm=
(3)由电磁感应中,流过杆ab的电量:q=
=
=
对于ab杆,由平衡条件:F=F安absinθ
而两棒所受的安培力大小相等,F安ab=F安ab;
则得:F=F安cdsinθ
由能量守恒:Fx=
m
+Qab+Qcd,
又 Qab=Qcd,
解得:Qab=Qcd=
=
答:(1)此时杆cd中的电流大小为
;
(2)杆ab的最大速度为
;
(3)若此过程中流过杆ab的电量为q,则cd产生的焦耳热Q为
.
mgsinθ=f
N+F安cd=mgcosθ
又有f=μN,F安cd=BIl
解得:F安cd=
| ||
| 6 |
| ||
| 6lB |
(2)根据闭合电路欧姆定律得知:ab棒产生的感应电动势为 E=I?2R=2IR;
由法拉第电磁感应定律得:E=Blvmsinθ
解得:vm=
2
| ||
| 3B2l2 |
(3)由电磁感应中,流过杆ab的电量:q=
| △φ |
| 2R |
| Bsinθ?x?l |
| 2R |
| Bxl |
| 4R |
对于ab杆,由平衡条件:F=F安absinθ
而两棒所受的安培力大小相等,F安ab=F安ab;
则得:F=F安cdsinθ
由能量守恒:Fx=
| 1 |
| 2 |
| v | 2m |
又 Qab=Qcd,
解得:Qab=Qcd=
| ||
| 6Bl |
| m3g2R2 |
| 3B4l4 |
答:(1)此时杆cd中的电流大小为
| ||
| 6lB |
(2)杆ab的最大速度为
2
| ||
| 3B2l2 |
(3)若此过程中流过杆ab的电量为q,则cd产生的焦耳热Q为
| m3g2R2 |
| 3B4l4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目