题目内容
【题目】如图所示，AB为固定在竖直面内、半径为R的四分之一圆弧形光滑轨道，其末端（B端）切线水平，且距水平地面的高度也为R； 1、2两小滑块（均可视为质点）用轻细绳拴接在一起，在它们中间夹住一个被压缩的微小轻质弹簧．两滑块从圆弧形轨道的最高点A由静止滑下，当两滑块滑至圆弧形轨道最低点时，拴接两滑块的细绳突然断开，弹簧迅速将两滑块弹开，滑块2恰好能沿圆弧形轨道运动到轨道的最高点A．已知R=0.45m，滑块1的质量m1=0.16kg，滑块2的质量m2=0.04kg，重力加速度g取10m/s2 ， 空气阻力可忽略不计．求：
（1）两滑块一起运动到圆弧形轨道最低点细绳断开前瞬间对轨道的压力的大小；
（2）在将两滑块弹开的整个过程中弹簧释放的弹性势能；
（3）滑块2的落地点与滑块1的落地点之间的距离．
【答案】
（1）
解：设两滑块一起滑至轨道最低点时的速度为v，所受轨道的支持力为N．对两滑块一起沿圆弧形轨道下滑到B端的过程，根据机械能守恒定律有：
（m1+m2）gR= 
（m1+m2）v2，
代入数据解得：v=3.0m/s
对于两滑块在轨道最低点，根据牛顿第二定律有：
N﹣（m1+m2）g=（m1+m2） 
解得：N=3（m1+m2）g=6.0N
根据牛顿第三定律可知，两滑块对轨道的压力大小为：N′=N=6.0N
（2）
解：设弹簧迅速将两滑块弹开时，两滑块的速度大小分别为v1和v2，因滑块2恰好能沿圆弧形轨道运动到轨道最高点A，此过程中机械能守恒，所以对滑块2有：
m2gR= m2v22
代入数据解得：v2=3.0m/s，方向向左
对于弹簧将两滑块弹开的过程，设水平向右为正方向，根据动量守恒定律有：
（m1+m2）v=m1v1﹣m2v2
代入数据解得：v1=4.5m/s
对于弹簧将两滑块弹开的过程，根据机械能守恒定律有：
E弹= m1v12+ m2v22﹣ （m1+m2）v2
代入数据解得：E弹=0.90J
（3）
解：设两滑块平抛运动的时间为t，根据h= gt2，
解得两滑块做平抛运动的时间为：t= 
=0.30s
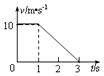
滑块1平抛的水平位移为：x1=v1t=1.35m
滑块2从B点上滑到A点，再从A点返回到B点的过程，机械能守恒，因此其平抛的速度大小仍为v2，所以其平抛的水平位移为：x2=v2t=0.90m
所以滑块2的落地点与滑块1的落地点之间的距离为：△x=x1﹣x2=0.45m
【解析】（1）12在下滑过程中机械能守恒求得到达底端的速度，根据牛顿第二定律求得与轨道的相互作用力；（2）对2根据机械能守恒求得弹簧弹开后的速度，利用动量定理求得1的速度，根据能量守恒求得弹簧的弹性势能；（3）12两物体做平抛运动，根据平抛运动的特点求得水平位移即可求得
【考点精析】通过灵活运用机械能守恒及其条件和动量守恒定律，掌握在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变；动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变即可以解答此题．
