题目内容
3.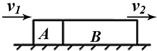 如图所示,木块A、B并排且固定在水平桌面上,A的长度是L,B的长度是3L,一颗子弹沿水平方向以速度v1射入A,以速度v2穿出B,子弹可视为质点,其运动视为匀变速直线运动,则子弹穿出A时的速度为( )
如图所示,木块A、B并排且固定在水平桌面上,A的长度是L,B的长度是3L,一颗子弹沿水平方向以速度v1射入A,以速度v2穿出B,子弹可视为质点,其运动视为匀变速直线运动,则子弹穿出A时的速度为( )| A. | $\frac{{v}_{2}+2{v}_{1}}{4}$ | B. | $\frac{{v}_{2}}{2}$ | C. | $\sqrt{\frac{{v}_{2}^{2}+3{v}_{1}^{2}}{4}}$ | D. | $\sqrt{\frac{{{v}_{2}}^{2}-3{{v}_{1}}^{2}}{4}}$ |
分析 子弹的运动为匀减速直线运动,所受摩擦力保持不变,而A的长度是L,B的长度是2L,所以摩擦力在穿过A的过程做的功是穿过B过程做功的一半,对子弹穿过AB的整个过程运用动能定理即可求出摩擦力在整个过程中做的功,再对子弹穿过A的过程运用动能定理即可求出子弹穿出A时的速度.
解答 解:设子弹的质量为m,对子弹穿过AB的整个过程运用动能定理得:$\frac{1}{2}m{v}_{2}^{2}$-$\frac{1}{2}m{v}_{1}^{2}$=Wf,
因为子弹所受摩擦力保持不变,又因为A的长度是L,B的长度是3L,所以子弹穿过A的过程中摩擦力做的功为$\frac{1}{4}$Wf,
对子弹穿过A的过程,由动能定理得:$\frac{1}{4}$Wf=$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}m{v}_{1}^{2}$,
解得:v=$\sqrt{\frac{{v}_{2}^{2}+3{v}_{1}^{2}}{4}}$
故选:C
点评 本题是对整体和隔离物体分别运用动能定理解题的典型例题,要能正确选取研究对象及运动过程,并能熟练地运用动能定理解题,难度适中.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
17.两个带电量大小之比为5:7的点电荷相聚R,它们之间的库仑力为F,现将两电荷接触后,再放回远处,则后来的库仑力大小为( )
| A. | $\frac{36}{35}$F | B. | $\frac{1}{35}$F | C. | $\frac{1}{2}$F | D. | $\frac{1}{12}$F |
14.某同学将质量为m的矿泉水瓶(可看成质点)竖直向上抛出,瓶以1.25g的加速度匀减速上升,上升的最大高度为H.水瓶往返过程受到的阻力大小不变,重力加速度为g,则( )
| A. | 上升过程中,瓶的动能改变量为1.25mgH | |
| B. | 上升过程中,瓶的机械能减少了0.25mgH | |
| C. | 瓶落回地面时动能大小为0.75mgH | |
| D. | 瓶上升过程处于超重状态,下落过程处于失重状态 |
1. 用力F向左推B球将弹簧压缩,如图所示.然后突然将力F撤去,在撤去力F的瞬间,A、B两球的加速度分别为( )
用力F向左推B球将弹簧压缩,如图所示.然后突然将力F撤去,在撤去力F的瞬间,A、B两球的加速度分别为( )
 用力F向左推B球将弹簧压缩,如图所示.然后突然将力F撤去,在撤去力F的瞬间,A、B两球的加速度分别为( )
用力F向左推B球将弹簧压缩,如图所示.然后突然将力F撤去,在撤去力F的瞬间,A、B两球的加速度分别为( )| A. | 0,0 | B. | 0,$\frac{F}{m}$ | C. | $\frac{F}{2m}$,$\frac{F}{m}$ | D. | $\frac{F}{2m}$,$\frac{F}{2m}$ |
12. 如图所示,A、B、C是两个等量异种点电荷连线的中垂线上的三点,设EA、EB、EC和ϕA、ϕB、ϕC分别为A、B、C三点的场强和电势,则( )
如图所示,A、B、C是两个等量异种点电荷连线的中垂线上的三点,设EA、EB、EC和ϕA、ϕB、ϕC分别为A、B、C三点的场强和电势,则( )
 如图所示,A、B、C是两个等量异种点电荷连线的中垂线上的三点,设EA、EB、EC和ϕA、ϕB、ϕC分别为A、B、C三点的场强和电势,则( )
如图所示,A、B、C是两个等量异种点电荷连线的中垂线上的三点,设EA、EB、EC和ϕA、ϕB、ϕC分别为A、B、C三点的场强和电势,则( )| A. | EA<EB<EC | B. | EA>EB>EC | C. | ϕA<ϕB<ϕC | D. | ϕA=ϕB=ϕC |
13.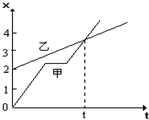 如图所示,甲、乙两质点在同一直线上的位移-时间图象(x-t图),以甲的出发点为原点,出发时间为计时的起点,则( )
如图所示,甲、乙两质点在同一直线上的位移-时间图象(x-t图),以甲的出发点为原点,出发时间为计时的起点,则( )
 如图所示,甲、乙两质点在同一直线上的位移-时间图象(x-t图),以甲的出发点为原点,出发时间为计时的起点,则( )
如图所示,甲、乙两质点在同一直线上的位移-时间图象(x-t图),以甲的出发点为原点,出发时间为计时的起点,则( )| A. | 在t时刻,甲追上了乙 | |
| B. | 甲、乙是从同一地点开始运动的 | |
| C. | 甲追上乙时,甲运动的速度比乙的小 | |
| D. | 乙的平均速度比甲的平均速度大 |
 如图所示,q1、q2、q3分别表示在同一直线上的三个点电荷,已知q1、q2间的距离为r,q2、q3间的距离为3r,且每一个点电荷都处于平衡状态.若q2是负电荷,则q1是正电荷,q2是正电荷.
如图所示,q1、q2、q3分别表示在同一直线上的三个点电荷,已知q1、q2间的距离为r,q2、q3间的距离为3r,且每一个点电荷都处于平衡状态.若q2是负电荷,则q1是正电荷,q2是正电荷.