题目内容
15.甲、乙两物体从同一位置沿同一直线运动,甲物体以10m/s的初速度做匀加速直线运动,加速度为a甲=1.5m/s2,达到最大速度40m/s后做匀速直线运动,乙物体从静止开始做匀加速直线运动,其加速度为a乙=2.0m/s2,甲运动20s后乙开始运动.求:(1)乙在追上甲前多长时间相距最远?此时他们之间的距离是多少?
(2)乙至少要用多长时间才能追上甲?
分析 (1)当甲乙的速度相等时,两者有最大距离,根据速度公式和位移公式求出最远距离.
(2)结合位移关系,运用运动学公式求出追及的时间.
解答 解:(1)甲物体达到最大速度用时${t}_{1}=\frac{v-{v}_{甲0}}{{a}_{甲}}=\frac{40-10}{1.5}s=20s$,
此时乙加速运动,当两者速度相等时,甲乙相距最远,
由v甲=v乙=a乙t乙得,t乙=20s.
此时甲运动的位移为${x}_{甲}=\frac{{v}_{甲0}+{v}_{甲}}{2}{t}_{1}+{v}_{甲}{t}_{乙}$,
代入数据解得x甲=1300m,
乙运动的位移为${x}_{乙}=\frac{{v}_{甲}}{2}{t}_{乙}$,代入数据解得x乙=400m.
所以甲乙相距的最大距离△x=x甲-x乙=1300-400m=900m.从乙开始运动计时,乙在追上甲前20s相距最远.
(2)乙追上甲时有:x甲=x乙,
即$\frac{{v}_{甲0}+{v}_{甲}}{2}{t}_{1}+{v}_{甲}t=\frac{1}{2}{a}_{乙}{t}^{2}$,
代入数据解得t=50s,t=-10s(舍去).
所以乙需要50s追上甲物体.
答:(1)乙在追上甲前20s时间相距最远,此时他们之间的距离是900m;
(2)乙至少要用50s时间才能追上甲.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式灵活求解,知道速度相等时有最大距离.

练习册系列答案
相关题目
8. 如图所示,一木箱置小孩用80N的水平力推重力为200N的木箱,木箱不动;当小孩用100N的水平力推木箱,木箱恰好能被推动;当木箱被推动之后,小孩只要用90N的水平推力就可以使木箱沿地面匀速前进,以下是对上述过程作出的计算和判断,其中正确的是( )
如图所示,一木箱置小孩用80N的水平力推重力为200N的木箱,木箱不动;当小孩用100N的水平力推木箱,木箱恰好能被推动;当木箱被推动之后,小孩只要用90N的水平推力就可以使木箱沿地面匀速前进,以下是对上述过程作出的计算和判断,其中正确的是( )
 如图所示,一木箱置小孩用80N的水平力推重力为200N的木箱,木箱不动;当小孩用100N的水平力推木箱,木箱恰好能被推动;当木箱被推动之后,小孩只要用90N的水平推力就可以使木箱沿地面匀速前进,以下是对上述过程作出的计算和判断,其中正确的是( )
如图所示,一木箱置小孩用80N的水平力推重力为200N的木箱,木箱不动;当小孩用100N的水平力推木箱,木箱恰好能被推动;当木箱被推动之后,小孩只要用90N的水平推力就可以使木箱沿地面匀速前进,以下是对上述过程作出的计算和判断,其中正确的是( )| A. | 木箱与地面间的动摩擦因数μ=0.45 | |
| B. | 木箱与地面间的最大静摩擦力大小为100N | |
| C. | 木箱与地面间的摩擦力大小始终为80N | |
| D. | 木箱与地面间的滑动摩擦力大小为90N |
3.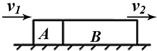 如图所示,木块A、B并排且固定在水平桌面上,A的长度是L,B的长度是3L,一颗子弹沿水平方向以速度v1射入A,以速度v2穿出B,子弹可视为质点,其运动视为匀变速直线运动,则子弹穿出A时的速度为( )
如图所示,木块A、B并排且固定在水平桌面上,A的长度是L,B的长度是3L,一颗子弹沿水平方向以速度v1射入A,以速度v2穿出B,子弹可视为质点,其运动视为匀变速直线运动,则子弹穿出A时的速度为( )
 如图所示,木块A、B并排且固定在水平桌面上,A的长度是L,B的长度是3L,一颗子弹沿水平方向以速度v1射入A,以速度v2穿出B,子弹可视为质点,其运动视为匀变速直线运动,则子弹穿出A时的速度为( )
如图所示,木块A、B并排且固定在水平桌面上,A的长度是L,B的长度是3L,一颗子弹沿水平方向以速度v1射入A,以速度v2穿出B,子弹可视为质点,其运动视为匀变速直线运动,则子弹穿出A时的速度为( )| A. | $\frac{{v}_{2}+2{v}_{1}}{4}$ | B. | $\frac{{v}_{2}}{2}$ | C. | $\sqrt{\frac{{v}_{2}^{2}+3{v}_{1}^{2}}{4}}$ | D. | $\sqrt{\frac{{{v}_{2}}^{2}-3{{v}_{1}}^{2}}{4}}$ |
10. 如图,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为v0)( )
如图,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为v0)( )
 如图,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为v0)( )
如图,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为v0)( )| A. | 若把斜面CB部分截去,物体冲过C点后上升的最大高度仍为h | |
| B. | 把斜面从C点以上部分弯成与C点相切的圆弧状,物体上升的最大高度有可能仍为h | |
| C. | 若把斜面弯成圆弧形D,物体仍沿圆弧升高h | |
| D. | 若把斜面AB变成曲面AEB,物体沿此曲面上升仍能到达B点 |
20.中俄共同签署了《中国国家航天局和俄罗斯联邦航天局关于联合探测火星一火卫一合作的协议》,双方确定联合对火星及其卫星“火卫一”进行探测.“火卫一”就在火星赤道正上方运行,与火星中心的距离为9450km.绕火星一周需7h39min,(万有引力常量G已知)若其绕行轨道可简化为圆形轨道,则由以上信息可以确定的是( )
| A. | 火卫一的质量 | B. | 火星的质量 | ||
| C. | 火卫一的绕行速度 | D. | 火卫一的向心加速度 |
4.某物体沿直线运动的v-t图象如图所示,由图可以看出物体( )


| A. | 沿直线向一个方向运动 | B. | 沿直线做往复运动 | ||
| C. | 加速度不变 | D. | t4时刻离出发点最远 |
 如图所示,一质量m1=0.6kg的小车静止在光滑的水平面上,现有一质量m2=0.3kg的物块,以水平向右的速度v0=6m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数0.4,取g=10m/s2,求:
如图所示,一质量m1=0.6kg的小车静止在光滑的水平面上,现有一质量m2=0.3kg的物块,以水平向右的速度v0=6m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数0.4,取g=10m/s2,求: