题目内容
16. 2012年6月6日,金星恰好运动到地球和太阳的连线上,如图所示.在地面上看,金星像一个小黑点出现在太阳的一侧,并且慢慢地在几个小时内跨越太阳的圆盘出现在太阳的另一侧,这便是天文学里最罕见的景象之一,被称为“金星凌日”.“金星凌日”每隔N年才会出现一次,若金星与地球绕太阳公转的轨道平面共面,两轨道均可视为圆形,则金星与地球的公转半径之比为( )
2012年6月6日,金星恰好运动到地球和太阳的连线上,如图所示.在地面上看,金星像一个小黑点出现在太阳的一侧,并且慢慢地在几个小时内跨越太阳的圆盘出现在太阳的另一侧,这便是天文学里最罕见的景象之一,被称为“金星凌日”.“金星凌日”每隔N年才会出现一次,若金星与地球绕太阳公转的轨道平面共面,两轨道均可视为圆形,则金星与地球的公转半径之比为( )| A. | ${({\frac{N}{N+1}})^{\frac{2}{3}}}$ | B. | ${({\frac{N-1}{N}})^{\frac{2}{3}}}$ | C. | ${({\frac{N}{N+1}})^{\frac{3}{2}}}$ | D. | ${({\frac{N-1}{N}})^{\frac{3}{2}}}$ |
分析 根据开普勒第三定律,金星和地球的轨道半径的三次方之比等于公转周期的平方之比,列式求解.
解答 解:根据开普勒第三定律,有
$\frac{{{R}^{3}}_{金}}{{{R}^{3}}_{地}}=\frac{{T}_{金}^{2}}{{T}_{地}^{2}}$ ①
“金星凌日”每隔N年才会出现一次,知
($\frac{2π}{{T}_{金}}-\frac{2π}{{T}_{地}}$)N=2π ②
已知T地=1年 ③
联立①②③解得$\frac{{R}_{金}}{{R}_{地}}$=$(\frac{N}{N+1})^{\frac{2}{3}}$
故选:A
点评 本题考查开普勒定律的应用,当然,也可根据万有引力等于向心力列式求解.

练习册系列答案
相关题目
6. 如图所示,质量相同的两小球a、b分别从斜面顶端A和斜面中点B沿水平方向抛出后,恰好都落在斜面底端,不计空气阻力,下列说法正确的是( )
如图所示,质量相同的两小球a、b分别从斜面顶端A和斜面中点B沿水平方向抛出后,恰好都落在斜面底端,不计空气阻力,下列说法正确的是( )
 如图所示,质量相同的两小球a、b分别从斜面顶端A和斜面中点B沿水平方向抛出后,恰好都落在斜面底端,不计空气阻力,下列说法正确的是( )
如图所示,质量相同的两小球a、b分别从斜面顶端A和斜面中点B沿水平方向抛出后,恰好都落在斜面底端,不计空气阻力,下列说法正确的是( )| A. | 小球a、b在空中飞行的时间之比为2:1 | |
| B. | 小球a、b抛出时的初速度大小之比为2:1 | |
| C. | 小球a、b到达斜面底端时的动能之比为4:1 | |
| D. | 小球a、b到达斜面底端时速度方向与斜面的夹角之比为1:1 |
7. 在地球表面处取这样几个点:北极点A、赤道上一点B、AB弧的中点C、过C点的纬线上取一点D,如图所示.则下列说法正确的是( )
在地球表面处取这样几个点:北极点A、赤道上一点B、AB弧的中点C、过C点的纬线上取一点D,如图所示.则下列说法正确的是( )
 在地球表面处取这样几个点:北极点A、赤道上一点B、AB弧的中点C、过C点的纬线上取一点D,如图所示.则下列说法正确的是( )
在地球表面处取这样几个点:北极点A、赤道上一点B、AB弧的中点C、过C点的纬线上取一点D,如图所示.则下列说法正确的是( )| A. | C、D两点的向心加速度相同 | B. | B、C两点的向心加速度相同 | ||
| C. | C、D两点的线速度相同 | D. | B、C、D三点的角速度相同 |
1.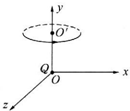 在如图所示的直角坐标系中,坐标原点O处固定有正点电荷,另有平行于y轴的匀强磁场.一个质量为m、带电量大小为q的微粒,恰能以y轴上O′点(O,a,O)为圆心作匀速圆周运动,其轨迹平面与xOz平面平行,角速度为ω,旋转方向如图中箭头所示.则以下说法正确的是( )
在如图所示的直角坐标系中,坐标原点O处固定有正点电荷,另有平行于y轴的匀强磁场.一个质量为m、带电量大小为q的微粒,恰能以y轴上O′点(O,a,O)为圆心作匀速圆周运动,其轨迹平面与xOz平面平行,角速度为ω,旋转方向如图中箭头所示.则以下说法正确的是( )
 在如图所示的直角坐标系中,坐标原点O处固定有正点电荷,另有平行于y轴的匀强磁场.一个质量为m、带电量大小为q的微粒,恰能以y轴上O′点(O,a,O)为圆心作匀速圆周运动,其轨迹平面与xOz平面平行,角速度为ω,旋转方向如图中箭头所示.则以下说法正确的是( )
在如图所示的直角坐标系中,坐标原点O处固定有正点电荷,另有平行于y轴的匀强磁场.一个质量为m、带电量大小为q的微粒,恰能以y轴上O′点(O,a,O)为圆心作匀速圆周运动,其轨迹平面与xOz平面平行,角速度为ω,旋转方向如图中箭头所示.则以下说法正确的是( )| A. | 微粒带负电 | |
| B. | 磁感应强度的方向可能沿+y轴,也可能沿-y轴 | |
| C. | 匀强磁场的磁感应强度的大小为$\frac{mg}{aqω}$+$\frac{mω}{q}$,方向沿-y轴 | |
| D. | 匀强磁场的磁感应强度的大小与固定的正点电荷电量有关,但方向一定沿-y轴 |
 宇宙中存在由质量相等的四颗星组成的四星系统,四星系统离其他恒星较远,通常可忽略其他星体对四星系统的引力作用.已观测到稳定的四星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为a的正方形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动,其运动周期为T1,如图(1)所示.另一种形式是有三颗星位于等边三角形的三个项点上,第四颗星刚好位于三角形的中心不动,三颗星沿等边三角形的半径为a的外接圆的圆形轨道运行,其运动周期为T2,如图(2)所示.试求两种形式下,星体运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$?
宇宙中存在由质量相等的四颗星组成的四星系统,四星系统离其他恒星较远,通常可忽略其他星体对四星系统的引力作用.已观测到稳定的四星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为a的正方形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动,其运动周期为T1,如图(1)所示.另一种形式是有三颗星位于等边三角形的三个项点上,第四颗星刚好位于三角形的中心不动,三颗星沿等边三角形的半径为a的外接圆的圆形轨道运行,其运动周期为T2,如图(2)所示.试求两种形式下,星体运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$?