Question

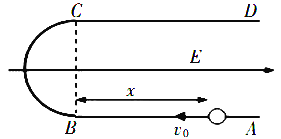
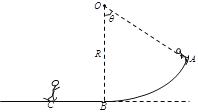
【题目】如图，A、B为半径R＝1 m的四分之一光滑绝缘竖直圆弧轨道，在四分之一圆弧区域内存在着E＝1×106V/m、竖直向上的匀强电场，有一质量m＝1 kg、带电荷量q＝＋1．4×10－5C的物体（可视为质点），从A点的正上方距离A点H处由静止开始自由下落（不计空气阻力），BC段为长L＝2 m、与物体间动摩擦因数μ＝0．2的粗糙绝缘水平面．（取g＝10 m/s2）

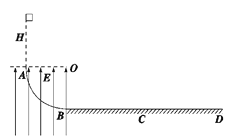
（1）若H＝1 m，物体能沿轨道AB到达最低点B，求它到达B点时对轨道的压力大小；

（2）通过你的计算判断：是否存在某一H值，能使物体沿轨道AB经过最低点B后最终停在距离B点0．8 m处。

Answer 1

【答案】（1）8 N（2）不存在某一H值，使物体沿着轨道AB经过最低点B后，停在距离B点0．8 m处．

【解析】试题分析：（1）物体由初始位置运动到B点的过程中根据动能定理有

mg（R＋H）－qER＝mv2

到达B点时由支持力FN、重力、电场力的合力提供向心力FN－mg＋qE＝

解得FN＝8 N

根据牛顿第三定律，可知物体对轨道的压力大小为8 N，方向竖直向下

（2）要使物体沿轨道AB到达最低点B，当支持力为0时，最低点有个最小速度v，则

qE－mg＝

解得v＝2 m/s

在粗糙水平面上，由动能定理得：－μmgx＝－mv2

所以x＝1 m>0．8 m

故不存在某一H值，使物体沿着轨道AB经过最低点B后，停在距离B点0．8 m处．