题目内容
【题目】如图所示,一圆球固定在水平地面上,球心为O。直细棒AB的B端搁在地面上,棒身靠在球面上并和球心在同一竖直平面内,切点为P,细棒与水平面之间的夹角为θ。若移动棒的B端沿水平地面靠近圆球,使切点P恰好以O点为圆心做匀速圆周运动,则
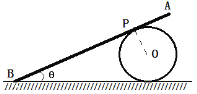
A.B端向右匀速运动B.θ角随时间均匀增大
C.PB长度随时间均匀减小D.以上说法都不对
【答案】B
【解析】
A.将B点速度沿着平行杆和垂直杆方向分解,如图所示: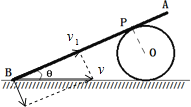
故
![]()
其中v1=vp,P点做匀速圆周运动,故vp不变,由于θ变大,故v变大,即B端向右加速,故A错误;
B.结合几何关系,经过时间t后的θ角增加为:
![]()
故θ角随时间均匀增大,故B正确;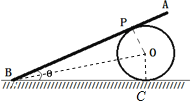
C.PB的长度等于CB的长度,由于B点向右是加速运动,故PB长度不是随时间均匀减小,故C错误;
D.由于B正确,故D错误;
故选B。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目