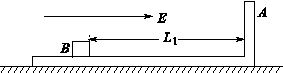题目内容
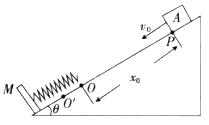
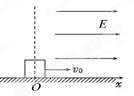
如图,绝缘水平地面上有宽L=0.4m的匀强电场区域,场强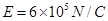 ,方向水平向左。带电的物块B静止在电场边缘的O点,带电量
,方向水平向左。带电的物块B静止在电场边缘的O点,带电量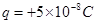 、质量
、质量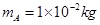 的物块A在距O点s=2.25m处以vo=5m/s的水平初速度向右运动,并与B发生碰撞,假设碰撞前后A、B构成的系统没有动能损失。A的质量是B的k(k>1)倍,A、B与地面间的动摩擦因数都为
的物块A在距O点s=2.25m处以vo=5m/s的水平初速度向右运动,并与B发生碰撞,假设碰撞前后A、B构成的系统没有动能损失。A的质量是B的k(k>1)倍,A、B与地面间的动摩擦因数都为 =0.2,物块均可视为质点,且A的电荷量始终不变,取g = 10m/S2。
=0.2,物块均可视为质点,且A的电荷量始终不变,取g = 10m/S2。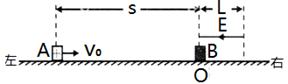
(1) 求A到达O点与B碰撞前的速度大小;
(2) 求碰撞后瞬间A和B的速度大小;
(3) 讨论K在不同取值范围时电场力对A做的功。
(1) 4m/s (2)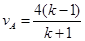 m/s
m/s 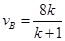 m/s (3)(i)当k>3时A能从电场右边界离开电场力对A做功为1.2×10-2 J;在1<k≤3范围内,A从电场的左侧离开,整个过程电场力做功为0。
m/s (3)(i)当k>3时A能从电场右边界离开电场力对A做功为1.2×10-2 J;在1<k≤3范围内,A从电场的左侧离开,整个过程电场力做功为0。
解析试题分析:(1)设碰撞前A的速度为v,由动能定理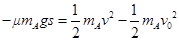 ①
①
得:  =4m/s ②
=4m/s ②
(2)设碰撞后A、B速度分别为vA、vB,且设向右为正方向;由于弹性碰撞,所以有: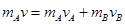 ③
③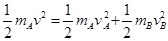 ④
④
联立③④并将mA=kmB及v=4m/s代入得: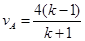 m/s ⑤
m/s ⑤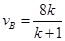 m/s ⑥
m/s ⑥
(3)讨论:
(i)如果A能从电场右边界离开,必须满足: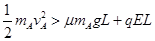 ⑦
⑦
联立⑤⑦代入数据,得: k>3 ⑧
电场力对A做功为:WE=-qEL=-6×105×5×10-8×0.4(J)=-1.2×10-2(J) ⑨
(ii)如果A不能从电场右边界离开电场,必须满足: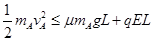 ⑩
⑩
联立⑤⑩代入数据,得:k≤3 ?
考虑到k>1,所以在1<k≤3范围内A不能从电场右边界离开 ?
又: qE=3×10-2N>μmg=2×10-2N ?
所以A会返回并从电场的左侧离开,整个过程电场力做功为0.即:WE=0 ?
考点:弹性碰撞 动量守恒 机械能守恒 动能定理