题目内容

如图所示，倾角为θ的斜面上只有AB段粗糙，其余部分都光滑，AB段长为3L．有若干个相同的小方块沿斜面靠在一起，但不粘接，总长为L．将它们由静止释放，释放时下端距A为2L．当下端运动到A下面距A为L/2时物块运动的速度达到最大．（单独研究一个小方块时可将其视为质点）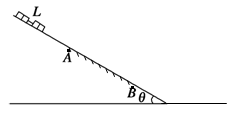

① 求物块与粗糙斜面的动摩擦因数；
② 求物块停止时的位置；
③ 要使所有物块都能通过B点，由静止释放时物块下端距A点至少要多远？　

（1）μ＝2tanθ；（2）物块的下端停在B端；（3）s＝3L

解析试题分析: (1)当整体所受合外力为零时，整体速度最大，设整体质量为m，则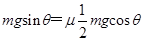
 
得μ＝2tanθ
(2)设物块停止时下端距A点的距离为x，根据动能定理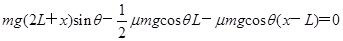
 
解得x＝3L  
即物块的下端停在B端  
(3)设静止时物块的下端距A的距离为s，物块的上端运动到A点时速度为v，根据动能定理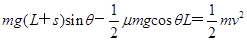
   
物块全部滑上AB部分后，小方块间无弹力作用，取最上面一块为研究对象，设其质量为m0，运动到B点时速度正好减到0，根据动能定理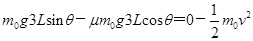
      得s＝3L  
考点： 动能定理

练习册系列答案
相关题目

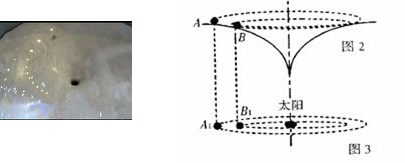
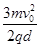坐标原点O处有一点状的放射源，它向xOy平面内的x轴上方各个方向发射α粒子，α粒子的速度大小都是v0，在0＜y＜d的区域内分布有指向y轴正方向的匀强电场，场强大小为E＝，其中q与m分别为α粒子的电荷量和质量；在d＜y＜2d的区域内分布有垂直于xOy平面的匀强磁场．ab为一块很大的平面感光板，放置于y＝2d处，如图所示．观察发现此时恰无粒子打到ab板上．(不考虑α粒子的重力)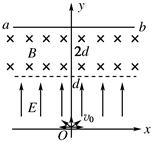

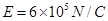(1)求α粒子刚进入磁场时的动能；
(2)求磁感应强度B的大小；
(3)将ab板平移到什么位置时所有粒子均能打到板上？并求出此时ab板上被α粒子打中的区域的长度．

如图，绝缘水平地面上有宽L=0.4m的匀强电场区域，场强，方向水平向左。带电的物块B静止在电场边缘的O点，带电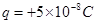量、质量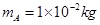的物块A在距O点s=2.25m处以vo=5m/s的水平初速度向右运动，并与B发生碰撞，假设碰撞前后A、B构成的系统没有动能损失。A的质量是B的k(k>1)倍，A、B与地面间的动摩擦因数都为=0.2，物块均可视为质点，且A的电荷量始终不变，取g = 10m/S2。

(1) 求A到达O点与B碰撞前的速度大小；
(2) 求碰撞后瞬间A和B的速度大小；
(3) 讨论K在不同取值范围时电场力对A做的功。

在天津市科技馆中，有一个模拟万有引力的装置。在如上图所示的类似锥形漏斗固定的容器中，有两个小球在该容器表面上绕漏斗中心轴做水平圆周运动，其运行能形象地模拟了太阳系中星球围绕太阳的运行。图2为示意图，图3为其模拟的太阳系运行图。图1中离中心轴的距离相当于行星离太阳的距离。则：

（1）在图3中，设行星A1和B1离太阳距离分别为r1和r2，求A1和B1运行速度大小之比。
（2）在图2中，若质量为m的A球速度大小为v，在距离中心轴为x1的轨道面上旋转，由于受到微小的摩擦阻力，A球绕轴旋转同时缓慢落向漏斗中心。当其运动到距离中心轴为x2的轨道面时，两轨道面之间的高度差为H。请估算此过程中A球克服摩擦阻力所做的功。

（18分）如图，一个质量为m的小球（可视为质点）以某一初速度从A点水平抛出，恰好从圆管BCD的B点沿切线方向进入圆弧，经BCD从圆管的最高点D射出，恰好又落到B点．已知圆弧的半径为R且A与D在同一水平线上，BC弧对应的圆心角θ=60°，不计空气阻力．求：

（1）小球从A点做平抛运动的初速度v0的大小；
（2）在D点处管壁对小球的作用力N；
（3）小球在圆管中运动时克服阻力做的功Wf．

如图所示，固定在水平面上的斜面与水平面的连接处为一极小的光滑圆弧(物块经过Q点时不损失机械能)，斜面与地面是用同种材料制成的。斜面的最高点为P，P距离水平面的高度为h=5m。在P点先后由静止释放两个可视为质点的小物块A和B，A、B的质量均为m=1kg，A与斜面及水平面的动摩擦因数为μ1=0.5，B与斜面及水平面的动摩擦因数为μ2=0.3。A物块从P点由静止释放后沿斜面滑下，停在了水平面上的某处。

求：
(1)A物块停止运动的位置距离斜面的直角顶端O点的距离是多少?
(2)当A物块停止运动后准备再释放B物块时发现它们可能会发生碰撞，为了避免AB碰撞，此时对A另外施加了一个水平向右的外力F，把A物体推到了安全的位置，之后再释放B就避免了AB碰撞。求外力F至少要做多少功，可使AB不相撞?(g取10m/s2，此问结果保留三位有效数字)

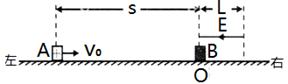
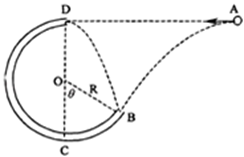
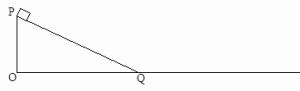
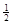（8分） 如图所示，质量为m的小球用长为L的轻质细线悬于O点，与O点处于同一水平线上的P点处有一根光滑的细钉，已知OP =L，在A点给小球一个水平向左的初速度v0，发现小球恰能到达跟P点在同一竖直线上的最高点B，则：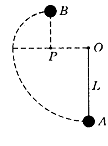

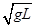（1）小球到达B点时的速度多大？
（2）若不计空气阻力，则初速度v0多大？
（3）若初速度v0=3，则在小球从A到B的过程中克服空气阻力做了多少功？

如图所示，在光滑绝缘水平面上B点的正上方O处固定一个质点，在水平面上的A点放另一个质点，两个质点的质量均为m，带电量均为+Q 。C为AB直线上的另一点（O、A、B、C位于同一竖直平面上），AO间的距离为L，AB和BC间的距离均为L/2，在空间加一个水平方向的匀强电场后A处的质点处于静止。试问：

(1)该匀强电场的场强多大？其方向如何？
(2)如给A处的质点一个指向C点的初速度v0 ，则该质点到达C点时的加速度和速度分别多大？

(15分)在一次国际城市运动会中，要求运动员从高为H的平台上A点，由静止出发，沿着动摩擦因数为μ的滑道向下运动到B点后水平滑出，最后落在水池中，如图所示，设滑道的水平距离为L，B点的高度h可由运动员自由调节(取g＝10m/s2)，求：

⑴运动员到达B点的速度与高度h的关系；
⑵运动员要达到最大水平运动距离，B点的高度h应调为多大？对应的最大水平距离smax为多少？
⑶若图中H＝4m，L＝5m，动摩擦因数μ＝0.2，则水平运动距离要达到7m，h值应为多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网