题目内容
(12分) 如图所示,竖直平面内的一半径R=0.50 m的光滑圆弧槽BCD,B点与圆心O等高,一水平面与圆弧槽相接于D点,质量m=0.10 kg的小球从B点正上方H=0.95 m高处的A点自由下落,由B点进入圆弧轨道,从D点飞出后落在水平面上的Q点,DQ间的距离x=2.4 m,球从D点飞出后的运动过程中相对水平面上升的最大高度h=0.80 m,g取g=10 m/s2,不计空气阻力,求: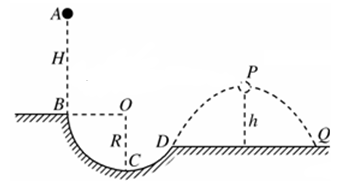
(1)小球经过C点时轨道对它的支持力大小FN;
(2)小球经过最高点P的速度大小vP;
(3)D点与圆心O的高度差hOD.
(1)6.8 N (2)3.0 m/s (3)0.30 m
解析试题分析:(1)设经过C点速度为v1,由机械能守恒有mg(H+R)=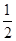 mv
mv
由牛顿第二定律有FN-mg=
代入数据解得:FN=6.8 N.
(2)P点时速度为vP, P到Q做平抛运动有h=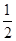 gt2,
gt2,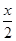 =vPt
=vPt
代入数据解得:vP=3.0 m/s.
(3)由机械能守恒定律,有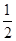 mv
mv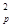 +mgh=mg(H+hOD),
+mgh=mg(H+hOD),
代入数据,解得hOD=0.30 m.
考点:本题考查机械能守恒、平抛运动规律。

练习册系列答案
相关题目
 时与另一小物块B发生碰撞并粘在一起以速度v飞离桌面,最终落在水平地面上。已知
时与另一小物块B发生碰撞并粘在一起以速度v飞离桌面,最终落在水平地面上。已知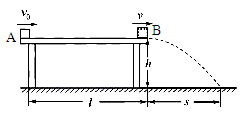
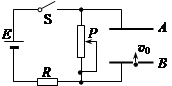
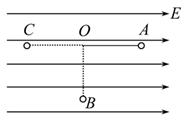
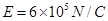 ,方向水平向左。带电的物块B静止在电场边缘的O点,带电量
,方向水平向左。带电的物块B静止在电场边缘的O点,带电量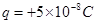 、质量
、质量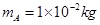 的物块A在距O点s=2.25m处以vo=5m/s的水平初速度向右运动,并与B发生碰撞,假设碰撞前后A、B构成的系统没有动能损失。A的质量是B的k(k>1)倍,A、B与地面间的动摩擦因数都为
的物块A在距O点s=2.25m处以vo=5m/s的水平初速度向右运动,并与B发生碰撞,假设碰撞前后A、B构成的系统没有动能损失。A的质量是B的k(k>1)倍,A、B与地面间的动摩擦因数都为 =0.2,物块均可视为质点,且A的电荷量始终不变,取g = 10m/S2。
=0.2,物块均可视为质点,且A的电荷量始终不变,取g = 10m/S2。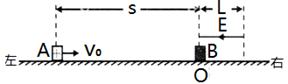
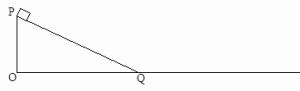
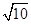 m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求
m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求 