题目内容
(12分)一个水平方向足够长的传送带以恒定的速度3 m/s沿顺时针方向转动,传送带右端固定着一个光滑曲面,并且与曲面相切,如图所示.小物块从曲面上高为h的P点由静止滑下,滑到传送带上继续向左运动,物块没有从左边滑离传送带。已知传送带与物体之间的动摩擦因数μ=0.2,不计物块滑过曲面与传送带交接处的能量损失,g取10 m/s2。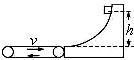
(1)若h1="1.25" m,求物块返回曲面时上升的最大高度。
(2)若h2="0.2" m,求物块返回曲面时上升的最大高度。
(1)0.45m (2)0.2m
解析试题分析:(1)设物块滑到下端的速度为v1,由动能定理得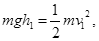
解得v1="5" m/s>3 m/s
所以物块先减速到速度为零后,又返回去加速运动,当两者的速度相同时,以共同的速度v="3" m/s一起匀速,直到滑上曲面.
由动能定理得物块上升的高度
(2)设物块滑到下端的速度为v2,由动能定理得 解得v2="2" m/s<3 m/s
解得v2="2" m/s<3 m/s
所以物块先减速到速度为零后,又返回去加速运动,又返回曲面时,速度仍为v2="2" m/s,然后滑上曲面,物块上升的高度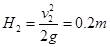
考点:本题考查了动能定理得应用

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
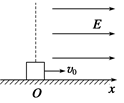
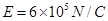 ,方向水平向左。带电的物块B静止在电场边缘的O点,带电量
,方向水平向左。带电的物块B静止在电场边缘的O点,带电量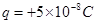 、质量
、质量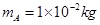 的物块A在距O点s=2.25m处以vo=5m/s的水平初速度向右运动,并与B发生碰撞,假设碰撞前后A、B构成的系统没有动能损失。A的质量是B的k(k>1)倍,A、B与地面间的动摩擦因数都为
的物块A在距O点s=2.25m处以vo=5m/s的水平初速度向右运动,并与B发生碰撞,假设碰撞前后A、B构成的系统没有动能损失。A的质量是B的k(k>1)倍,A、B与地面间的动摩擦因数都为 =0.2,物块均可视为质点,且A的电荷量始终不变,取g = 10m/S2。
=0.2,物块均可视为质点,且A的电荷量始终不变,取g = 10m/S2。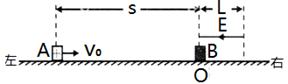
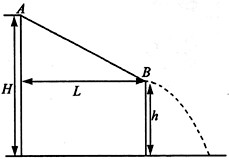
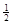 L,在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B,则:
L,在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B,则:
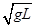 ,则在小球从A到B的过程中克服空气阻力做了多少功?
,则在小球从A到B的过程中克服空气阻力做了多少功?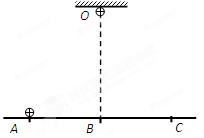

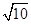 m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求
m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求