题目内容
(11分)光滑水平面上放有如图所示的用绝缘材料制成的“┙”型滑板（平面部分足够长），滑板的质量为4m。距离滑板的右壁A为L1的B处放有一质量为m、电量为+q(q>0)的小物体（可视为质点），小物体与板面之间的摩擦可忽略不计。整个装置处于场强为E、方向水平向右的匀强电场中。开始时，滑板与小物体都处于静止状态，某时刻释放小物体，求：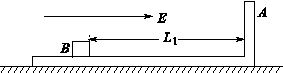
（1）小物体第一次跟滑板的A壁碰撞前瞬间的速度v1多大;
（2）若小物体与A壁碰撞时间极短，且碰撞过程没有机械能损失，则
a.小物体第二次即将跟A壁碰撞瞬间，滑板的速度v和小物体的速度v2分别为多大;
b.从开始释放小物体到它即将第二次跟A壁碰撞的过程中，整个装置的电势能减少了多少.
（1）
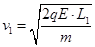（2）a.
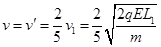;b: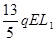
解析试题分析：由动能定理得：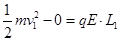
1分
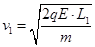得 1分
（2）a．小物体与A壁碰撞时间极短，且碰撞过程没有机械能损失
由动量守恒得
1分
机械能守恒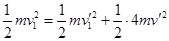
1分
可得
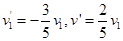1分
设再经过t发生第二次碰撞，则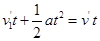
1分
可得
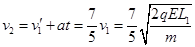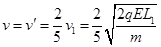1分 1分
b.小物块跟A壁第一次碰撞后到即将第二次跟A壁碰撞的过程中，滑板的位移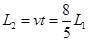
1分
小物体从释放到即将第二次跟A壁碰撞过程中
电场力对它所做的功：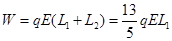
1分
所以整个装置的电势能减少量ΔE=W=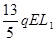 1分
考点：考查了动能定理，机械嫩守恒定律，动量守恒定律综合应用
练习册系列答案
相关题目
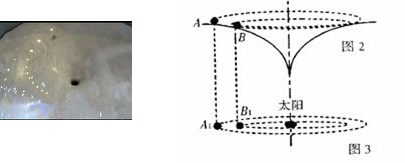
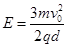，其中q与m分别为α粒子的电荷量和质量；在d＜y＜2d的区域内分布有垂直于xOy平面的匀强磁场．ab为一块很大的平面感光板，放置于y＝2d处，如图所示．观察发现此时恰无粒子打到ab板上．(不考虑α粒子的重力)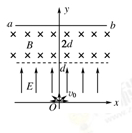
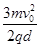，其中q与m分别为α粒子的电荷量和质量；在d＜y＜2d的区域内分布有垂直于xOy平面的匀强磁场．ab为一块很大的平面感光板，放置于y＝2d处，如图所示．观察发现此时恰无粒子打到ab板上．(不考虑α粒子的重力)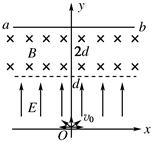
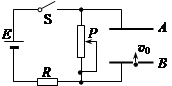
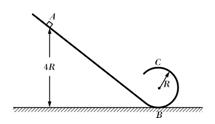
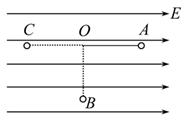
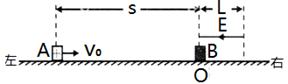
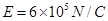，方向水平向左。带电的物块B静止在电场边缘的O点，带电量
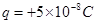、质量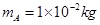
的物块A在距O点s=2.25m处以vo=5m/s的水平初速度向右运动，并与B发生碰撞，假设碰撞前后A、B构成的系统没有动能损失。A的质量是B的k(k>1)倍，A、B与地面间的动摩擦因数都为
=0.2，物块均可视为质点，且A的电荷量始终不变，取g = 10m/S2。
