题目内容
(12分)如图所示,在xoy坐标平面的第一象限内有沿-y方向的匀强电场,在第四象限内有垂直于平面向外的匀强磁场。现有一质量为m,带电量为-q的粒子(重力不计)以初速度v0沿-x方向从坐标为(3L、L)的P点开始运动,接着进入磁场,最后由坐标原点射出,射出时速度方向与y轴方间夹角为45º,求:
(1)粒子从O点射出时的速度v和电场强度E;
(2)粒子从P点运动到O点过程所用的时间。
(1)粒子在电场中做类平抛运动,在磁场中作圆周运动。到达O点时的速度与平抛运动末速度大小相等,方向都与水平方向成45º角。则平抛运动末速度的竖直分速度v⊥与水平分速度v都为![]() v0,且有平抛阶段的水平位移是竖直位移的两倍。
v0,且有平抛阶段的水平位移是竖直位移的两倍。
对类平抛过程,有: ![]()
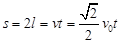
根据功能关系有: ![]()
其中s为平抛水平射程,t为平抛时间。
解得:v=![]() v0,
v0,![]()
(2)设R为粒子在磁场中做圆周运动的轨道半径,由几何知识可知圆弧所对圆心角为90º,则R=![]() l
l
粒子从O点运动到P点过程所用的时间等于在电场中做类平抛运动的时间与在磁场中运动四分之一圆周的时间之和,则:
总时间为:t总=t+![]() =
=![]() 。
。
解析:略

练习册系列答案
相关题目
 如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形,g=10m/s2)
如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形,g=10m/s2) 如图所示,在竖直平面的xoy坐标系中,oy竖直向上,ox水平.该平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿oy方向竖直向上抛出,初速度为V0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形)求:
如图所示,在竖直平面的xoy坐标系中,oy竖直向上,ox水平.该平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿oy方向竖直向上抛出,初速度为V0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形)求: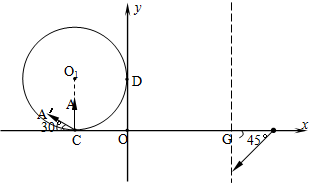 D点进入电场,最后从G点以与x轴正向夹角为45°的方向射出电场.求:
D点进入电场,最后从G点以与x轴正向夹角为45°的方向射出电场.求:
