题目内容
 如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形,g=10m/s2)
如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形,g=10m/s2)求:(1)在图中定性画出小球的运动轨迹并标出小球落回x轴时的位置N.
(2)小球到达N点的速度v2的大小.
分析:(1)根据竖直方向运动的对称性,结合运动的合成与分解,则有可求出水平方向运动的位移,从而确定N点的坐标;
(2)根据运动分解可知,竖直方向竖直上抛,水平方向做初速度为零的匀加速直线运动,结合分运动的等时性,运用运动学公式,即可求解.
(2)根据运动分解可知,竖直方向竖直上抛,水平方向做初速度为零的匀加速直线运动,结合分运动的等时性,运用运动学公式,即可求解.
解答:解:(1)由竖直方向的时间对称性可知,小球再经过t1回到x轴,水平方向从O点做初速度为零的匀加速直线运动,
上升与下落的时间相等,由于水平方向做初速度为零的匀加速直线运动,
根据在相同时间内,位移之比为1:3,则有:再回到x轴时落到x=12处,
所以位置N的坐标为(12,0).

(2)由竖直上抛运动的对称性知:到N点时竖直分速度大小为v0=4 m/s,
由v0=gt1得上升时间为:t1=0.4 s
由h=
gt2得上升的最大高度为:h=0.8 m
故图中每一小格为0.4 m
水平方向上:由:x=
at2
得:a=15m/s2
水平分速度:vx=atN=2at1=12 m/s,
故:v2=
=4
m/s
答:(1)在图中定性画出小球的运动轨迹如上图所示,并标出小球落回x轴时的位置N的坐标为(12,0).
(2)小球到达N点的速度v2的大小4
m/s.
上升与下落的时间相等,由于水平方向做初速度为零的匀加速直线运动,
根据在相同时间内,位移之比为1:3,则有:再回到x轴时落到x=12处,
所以位置N的坐标为(12,0).

(2)由竖直上抛运动的对称性知:到N点时竖直分速度大小为v0=4 m/s,
由v0=gt1得上升时间为:t1=0.4 s
由h=
| 1 |
| 2 |
故图中每一小格为0.4 m
水平方向上:由:x=
| 1 |
| 2 |
得:a=15m/s2
水平分速度:vx=atN=2at1=12 m/s,
故:v2=
| v02+vx2 |
| 10 |
答:(1)在图中定性画出小球的运动轨迹如上图所示,并标出小球落回x轴时的位置N的坐标为(12,0).
(2)小球到达N点的速度v2的大小4
| 10 |
点评:解答本题时要注意以下三点:小球竖直方向做竖直上抛运动,水平方向做匀加速运动;M点为最高点,则竖直方向的分速度为零;竖直方向的运动具有对称性.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 (2008?广州二模)如图所示,在竖直平面内有水平向右的匀强电场,同一竖直平面内水平拉直的绝缘细线一端系一带正电的小球,另一端固定于0点,已知带电小球受到的电场力大于重力,小球由静止释放,到达图中竖直虚线前小球做( )
(2008?广州二模)如图所示,在竖直平面内有水平向右的匀强电场,同一竖直平面内水平拉直的绝缘细线一端系一带正电的小球,另一端固定于0点,已知带电小球受到的电场力大于重力,小球由静止释放,到达图中竖直虚线前小球做( ) 如图所示,在竖直平面内有一边长为L的正方形区域处在场强为E的匀强电场中,电场方向与正方形一边平行.一质量为m、带电量为q的小球由某一边的中点,以垂直于该边的水平初速V0进入该正方形区域.当小球再次运动到该正方形区域的边缘时,具有的动能可能为( )
如图所示,在竖直平面内有一边长为L的正方形区域处在场强为E的匀强电场中,电场方向与正方形一边平行.一质量为m、带电量为q的小球由某一边的中点,以垂直于该边的水平初速V0进入该正方形区域.当小球再次运动到该正方形区域的边缘时,具有的动能可能为( ) 如图所示,在竖直平面内有一半圆形轨道,圆心为O,一质点小球从与圆心等高的圆形轨道上的A点以速度v0水平向右抛出,落于圆轨道上的C点,已知OC的连线与OA的夹角为θ,求小球从A到C的时间t=?(空气阻力不计)
如图所示,在竖直平面内有一半圆形轨道,圆心为O,一质点小球从与圆心等高的圆形轨道上的A点以速度v0水平向右抛出,落于圆轨道上的C点,已知OC的连线与OA的夹角为θ,求小球从A到C的时间t=?(空气阻力不计) 如图所示,在竖直平面内有一个粗糙的
如图所示,在竖直平面内有一个粗糙的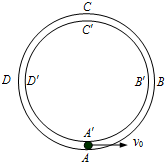 如图所示,在竖直平面内固定两个很靠近的同心圆形轨道,外轨道ABCD光滑,内轨道A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑,一质量m=0.2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,已知圆形轨道的半径R=0.32m,取g=10m/s2.
如图所示,在竖直平面内固定两个很靠近的同心圆形轨道,外轨道ABCD光滑,内轨道A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑,一质量m=0.2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,已知圆形轨道的半径R=0.32m,取g=10m/s2.