Question

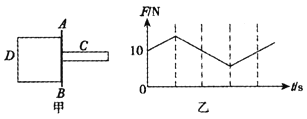
【题目】如图甲所示为阿特武德机的示意图，它是早期测量重力加速度的器械，由英国数学家和物理学家阿特武德于1784年制成。实验时将质量同为M(已知量)的重物用绳连接后，放在光滑的轻质滑轮上，处于静止状态。再在一个重物上附加一质量为m的小重物，由于小重物的重力而使系统做初速度为零的缓慢加速运动并测出加速度，完成一次实验后，换用不同质量的小重物，重复实验，测出不同m时系统的加速度。

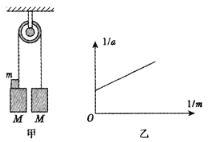
(1)如图甲左侧物块从静止开始下落，则为了得到图乙，需要直接测量的物理量有___________

A.小重物的质量m

B.大重物质量M

C.绳子的长度

D.重物下落的距离及下落这段距离所用的时间

(2)给过多次重复实验，得到多组a、m数据，作出图象，如图乙所示，已知该图象斜率为k，纵轴截距为b，则可求出当地的重力加速度g=__________，并可求出重物质量M=__________。

Answer 1

【答案】AD

【解析】

根据加速度的表达式，结合位移时间公式求出重力加速度的表达式，通过表达式确定所需测量的物理量．根据加速度的表达式得出关系式，通过图线的斜率和截距求出重力加速度和M的大小；

(1)对整体分析，根据牛顿第二定律得：，解得：，根据，则有：，所以需要测量的物理量有：小重物的质量m，重物下落的距离及下落这段距离所用的时间，故A、D正确，B、C错误；

故选AD。

(2)因为，则，知图线斜率，纵轴截距为， 解得当地的重力加速度，重物质量。