题目内容
【题目】如图所示,在光滑水平面上有一光滑小孔O;一根轻绳穿过小孔,一端连接质量为m=1kg的小球A,另一端连接质量为M=4kg的重物B。(g=10m/s2)
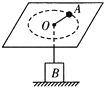
(1)当小球A沿半径r=0.1m的圆周做匀速圆周运动,其角速度为ω=10rad/s,物体B对地面的压力为多大?
(2)当A球的角速度为多大时,B物体处于将要离开而尚未离开地面的临界状态?
【答案】(1)30N(2)20rad/s
【解析】(1)以物体A为研究对象,由向心力公式可得绳子的张力
T=mω2r=1×102×0.1 N=10 N.
以物体B为研究对象,由平衡条件可得地面对B的支持力
N=Mg-T=(40-10) N=30 N.
根据牛顿第三定律可得物体B对地面的压力为30 N.
(2)B物体处于将要离开而尚未离开地面的临界状态,意味着地面对B的支持力为零,此时绳子的张力的大小等于B物体的重力,即T′=Mg=40 N.
A物体满足的关系为T′=mω′2r
进一步推导可得A球的角速度:
ω′=![]() =
=![]() rad/s=20 rad/s.
rad/s=20 rad/s.
思路分析:以物体A为研究对象,由向心力公式可得绳子的张力,以物体B为研究对象,由平衡条件可得地面对B的支持力,B物体处于将要离开而尚未离开地面的临界状态,意味着地面对B的支持力为零,此时绳子的张力的大小等于B物体的重力,即T′=Mg

练习册系列答案
相关题目