题目内容
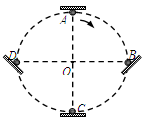
图甲为竖直放置的离心轨道,其中圆轨道的半径r=0.10m,在轨道的最低点A和最高点B各安装了一个压力传感器(图中未画出),小球(可视为质点)从斜轨道的不同高度由静止释放,可测出小球在轨道内侧通过这两点时对轨道的压力FA和FB。g取10m/s2。
(1)若不计小球所受阻力,且小球恰能过B点,求小球通过A点时速度vA的大小;
(2)若不计小球所受阻力,小球每次都能通过B点,FB随FA变化的图线如图乙中的a所示,求小球的质量m;
(3)若小球所受阻力不可忽略,FB随FA变化的图线如图乙中的b所示,求当FB=6.0N时,小球从A运动到B的过程中损失的机械能 。
。
(1)vA=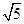 m/s (2)m=0.1kg (3)ΔE=0.2J
m/s (2)m=0.1kg (3)ΔE=0.2J
解析试题分析:(1)若小球恰能通过B点,
设此时小球质量为m,通过B时的速度为vB。
根据牛顿第二定律有
mg=mvB2/r
根据机械能守恒定律有
mvA2/2=mvB2/2+mg2r
所以 vA=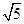 m/s
m/s
(2)根据第(1)问及图乙可知:当小球通过A点时的速度vA=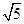 m/s时,小球对轨道压力的大小FA1=6N。设小球通过A点时,轨道对小球支持力的大小为FA2。
m/s时,小球对轨道压力的大小FA1=6N。设小球通过A点时,轨道对小球支持力的大小为FA2。
根据牛顿运动定律有
FA1=FA2 且 FA2-mg=mvA2/r
所以 m=0.1kg
(3)根据图乙可知:当小球通过B点时,若小球对轨道压力的大小FB=6.0N,则小球通过A点时对轨道压力的大小FA=16N。设轨道对小球通过A、B时支持力的大小分别为FA’、FB\,速度分别为va\、v\B据牛顿运动定律有
FA\=FA 且 FA\-mg=mvA\2/r
且 FA\-mg=mvA\2/r FB\=FB 且 FB\+mg=mvB2=mvB\2/r
FB\=FB 且 FB\+mg=mvB2=mvB\2/r
在小球从A运动到C的过程中,根据功能原理又有
mvA\2/2= mvB\2/2+mg2r+ΔE
所以 ΔE=0.2J
考点:本题考查牛顿第二定律、机械能守恒定律、能量守恒定律的应用。

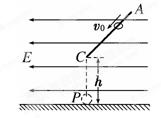
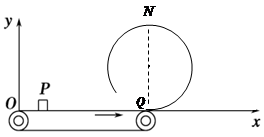
如图,一条形磁铁放在水平桌面上,在它的正中央上方固定一直导线,导线与磁铁垂直,若给导线通以垂直于纸面向里的电流,则 ( )
| A.磁铁对桌面的压力增大 | B.磁铁对桌面的压力减少 |
| C.桌面对磁铁没有摩擦力 | D.磁铁所受的合力不变 |


 .
.