题目内容
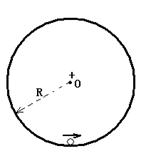
如图所示,x轴与水平传送带重合,坐标原点O在传送带的左端,传送带长L=8m,传送带右端Q点和竖直光滑圆轨道的圆心在同一竖直线上,皮带匀速运动的速度v0=5m/s。一质量m=1kg的小物块轻轻放在传送带上xP=2m的P点,小物块随传送带运动到Q点后恰好能冲上光滑圆弧轨道的最高点N点。小物块与传送带间的动摩擦因数μ=0.5,重力加速度g=10 m/s2。求: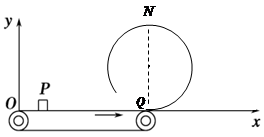
(1)N点的纵坐标;
(2)从P点到Q点,小物块在传送带上运动系统产生的热量;
(3)若将小物块轻放在传送带上的某些位置,小物块均能沿光滑圆弧轨道运动(小物块始终在圆弧轨道运动不脱轨)到达纵坐标yM=0.25m的M点,求这些位置的横坐标范围。
1m 12.5J 7m≤x≤7 .5m和0≤x≤5 .5m
解析试题分析:可先求出P到Q过程的加速度,在根据运动学公式列式求解出Q点的速度;在N点,重力恰好提供向心力,根据牛顿第二定律和匀速圆周运动公式可求出半径,求出摩擦力和相对位移可根据Q=f?△S求出热量.当物块能到达N点时不会脱离轨道,若能到达的高度超过半径又没到达N点则会脱离轨道,若能到达高度不超过半径则不会脱离轨道,可根据能量守恒求出对应的位移,从而求出坐标;
小物块在传送带上的加速度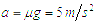
小物块与传送带共速时,所用的时间
运动的位移
故有:
由机械能守恒定律得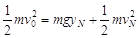 ,解得
,解得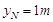
(2)小物块在传送带上相对传送带滑动的位移
产生的热量
(3)设在坐标为x1处将小物块轻放在传送带上,若刚能到达圆心右侧的M点,由能量守恒得:
μmg(L-x1)=mgyM
代入数据解得x1=7.5 m
μmg(L-x2)=mgyN
代入数据解得x2=7 m
若刚能到达圆心左侧的M点,由(1)可知x3=5.5 m
考点:机械能守恒定律;牛顿第二定律;向心力;能量守恒定律.

 阅读快车系列答案
阅读快车系列答案在真空中有A和B两个点电荷,它们所带电荷分别为QA和QB,如果QA=5QB,则A电荷受到B电荷的作用力是B电荷受到A电荷作用力的
| A.1倍 | B. 倍 倍 | C.5倍 | D.25倍 |

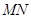 、
、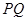 相距为
相距为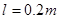 ,三根质量均为
,三根质量均为 的导体棒
的导体棒 、
、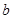 、
、 相距一定距离垂直放在导轨上且与导轨间动摩擦因数均为
相距一定距离垂直放在导轨上且与导轨间动摩擦因数均为 ,导体棒
,导体棒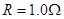 ,导体棒
,导体棒 。有磁感应强度为
。有磁感应强度为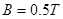 的范围足够大的匀强磁场垂直于导轨平面方向向上。现用一平行于导轨水平向右的足够大的拉力F作用在导体棒
的范围足够大的匀强磁场垂直于导轨平面方向向上。现用一平行于导轨水平向右的足够大的拉力F作用在导体棒 上,使之由静止开始向右做加速运动,导体棒始终与导轨垂直且接触良好,设最大静摩擦力等于滑动摩擦力,忽略导体棒间的相互作用,求:
上,使之由静止开始向右做加速运动,导体棒始终与导轨垂直且接触良好,设最大静摩擦力等于滑动摩擦力,忽略导体棒间的相互作用,求:
 刚开始运动时,导体棒
刚开始运动时,导体棒 ,撤去拉力F后导体棒
,撤去拉力F后导体棒

 。
。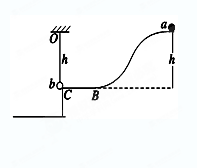
 .现在两小环沿杆向下移动至A′B′,使其在竖直方向上均下移h距离,同时释放两环.整个过程未超出弹簧的弹性限度,重力加速度为g,试求:
.现在两小环沿杆向下移动至A′B′,使其在竖直方向上均下移h距离,同时释放两环.整个过程未超出弹簧的弹性限度,重力加速度为g,试求: