Question

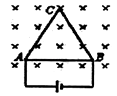
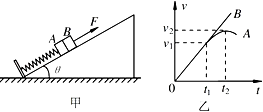
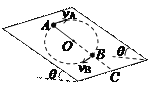
【题目】如图所示，在倾角为θ的光滑斜面上，有一长为l的细线，细线的一端固定在O点，另一端拴一质量为m的小球，现使小球恰好能在斜面上做完整的圆周运动，已知O点到斜面底边的距离为L，求：

（1）小球通过最高点A时的速度vA；

（2）小球通过最低点B时，细线对小球的拉力T；

（3）若小球运动到B点时细线断裂，小球滑落到斜面底边时到C点（C点为AB连线与底边的交点）的距离。

Answer 1

【答案】 6mgsinθ

【解析】试题分析：小球恰好能在斜面上做完整的圆周运动，在A点时重力的下滑分量恰好提供向心力，运动过程机械能守恒，最后结合类似平抛运动的知识列式即可求解。

（1）小球恰好能在斜面上做完整的圆周运动，则小球通过A点时细线的拉力为零，根据向心力公式有：

解得：

（2）小球从A点运动到B点，根据机械能守恒定律有：

解得：

小球在B点时根据向心力公式有：

解得：T＝6mgsinθ

（3）小球运动到B点时细线断裂，小球在平行底边方向做匀速运动，在垂直底边方向做初速为零的匀加速度运动，有：

x＝vBt

解得：x＝。