题目内容
【题目】如图，在光滑水平面上，放着两块长度相同，质量分别为M1和M2的木板，在两木板的左端各放一个大小、形状、质量完全相同的物块．开始时，各物均静止，今在两物体上各作用一水平恒力F1、F2 ， 当物块和木板分离时，两木板的速度分别为v1和v2 ， 物体和木板间的动摩擦因数相同，下列说法正确的是（ ）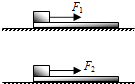
A.若F1=F2 ， M1＞M2 ， 则v1＞v2
B.若F1=F2 ， M1＜M2 ， 则v1＞v2
C.若F1＞F2 ， M1=M2 ， 则v1＞v2
D.若F1＜F2 ， M1=M2 ， 则v1＞v2
【答案】B,D
【解析】解：A、B：首先看F1=F2 时情况：
由题很容易得到两物块所受的摩擦力大小是相等的，因此两物块的加速度相同，我们设两物块的加速度大小为a，
对于M1、M2 ， 滑动摩擦力即为它们的合力，设M1的加速度大小为a1 ， M2的加速度大小为a2 ，
根据牛顿第二定律得：
因为a1= 
，a2= 
，其中m为物块的质量．
设板的长度为L，它们向右都做匀加速直线运动，当物块与木板分离时：
物块与M1的相对位移L= 
at12﹣ a1t12
物块与M2的相对位移L= at22﹣ a2t22
若M1＞M2 ， a1＜a2
所以得：t1＜t2
M1的速度为v1=a1t1 ， M2的速度为v2=a2t2
则v1＜v2 ， 故A错误．
若M1＜M2 ， a1＞a2
所以得：t1＞t2
M1的速度为v1=a1t1 ， M2的速度为v2=a2t2
则v1＞v2 ， 故B正确．
C、D：若F1＞F2、M1=M2 ， 根据受力分析和牛顿第二定律的：
则M1上的物块的加速度大于M2上的物块的加速度，即aa＞ab
由于M1=M2 ， 所以M1、M2加速度相同，设M1、M2加速度为a．
它们向右都做匀加速直线运动，当物块与木板分离时：
物块与M1的相对位移L= aat12﹣ at12
物块与M2的相对位移L= abt22﹣ at22
由于aa＞ab
所以得：t1＜t2
则v1＜v2 ， 故C错误．
若F1＜F2、M1=M2 ， aa＜ab
则v1＞v2 ， 故D正确．
故选BD．
【考点精析】本题主要考查了滑动摩擦力的相关知识点，需要掌握滑动摩擦力:利用公式f=μF N 进行计算，其中FN 是物体的正压力，不一定等于物体的重力，甚至可能和重力无关.或者根据物体的运动状态，利用平衡条件或牛顿定律来求解才能正确解答此题．
