题目内容
8. 如图所示,一束截面为圆形半径为R的平行单色光,垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形亮区,已知玻璃半球的半径为尺,屏幕S到球心的距离为d(d>3R),不考虑光的干涉和衍射,玻璃对该光的折射率为n,求
如图所示,一束截面为圆形半径为R的平行单色光,垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形亮区,已知玻璃半球的半径为尺,屏幕S到球心的距离为d(d>3R),不考虑光的干涉和衍射,玻璃对该光的折射率为n,求(1)屏幕上被照亮区域的半径;
(2)若将题干中单色光改为白光,在屏幕S上形成的圆形亮区的边缘是什么颜色?
分析 (1)光线沿直线从O点穿过玻璃,方向不变.从A点射出玻璃砖的光线方向向右偏折,射到屏幕S上圆形亮区,作出光路图,由光的折射定律结合数学几何知识求出圆形亮区的半径.
(2)当光线从空气垂直射入半圆玻璃砖,光线不发生改变,当入射角小于临界角时,光线才能再从玻璃砖射出,所以平行白光中的折射率不同,导致临界角不同,因此偏折程度不同,从而确定圆形亮区的最外侧的颜色;
解答 解:(1)如图,单色光刚要发生全反射时的临界光线射在屏幕S上的点E到亮区中心G的距离r就是所求最大半径.设单色光临界角为C,
由全反射的知识得:sinC=,
又:AB=RsinC=,
OB=RcosC=R,BF=AB•tanC=,GF=d-(OB+BF)=d-,
所以有r=GE=•AB=d•-nR
(2)紫色.当平行光从玻璃中射向空气时,由于紫光的折射率的最大,则临界角最小,所以首先发生全反射,因此出射光线与屏幕的交点最远.故圆形亮区的最外侧是紫光.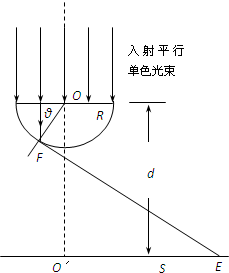
答:(1)若玻璃半球对(1)中最外侧色光的折射率为n,圆形亮区的最大半径为d•-nR.
(2)屏幕S上形成的圆形亮区的最外侧是紫光;
点评 本题考查光的折射.关键是作出光路图,根据几何知识求出入射角与折射角,知道折射率和临界角的关系,了解各种色光的波长和折射率的关系.

练习册系列答案
相关题目
3. 如图所示,放在水平地面上的底座C上插着光滑竖直杆MN.一根轻绳跨过轻质滑轮,一端悬吊的物体A,另一端与套在MN的小球B相连,不计轻绳与滑轮摩擦.系统达到平衡后,绳右侧与水平方向的夹角为θ,小球B与竖直杆间的弹力为F1,地面对底座的弹力和摩擦力分别为F2和F3.现在将底座向右侧移动少许,重新达到平衡后,下列说法正确的是( )
如图所示,放在水平地面上的底座C上插着光滑竖直杆MN.一根轻绳跨过轻质滑轮,一端悬吊的物体A,另一端与套在MN的小球B相连,不计轻绳与滑轮摩擦.系统达到平衡后,绳右侧与水平方向的夹角为θ,小球B与竖直杆间的弹力为F1,地面对底座的弹力和摩擦力分别为F2和F3.现在将底座向右侧移动少许,重新达到平衡后,下列说法正确的是( )
 如图所示,放在水平地面上的底座C上插着光滑竖直杆MN.一根轻绳跨过轻质滑轮,一端悬吊的物体A,另一端与套在MN的小球B相连,不计轻绳与滑轮摩擦.系统达到平衡后,绳右侧与水平方向的夹角为θ,小球B与竖直杆间的弹力为F1,地面对底座的弹力和摩擦力分别为F2和F3.现在将底座向右侧移动少许,重新达到平衡后,下列说法正确的是( )
如图所示,放在水平地面上的底座C上插着光滑竖直杆MN.一根轻绳跨过轻质滑轮,一端悬吊的物体A,另一端与套在MN的小球B相连,不计轻绳与滑轮摩擦.系统达到平衡后,绳右侧与水平方向的夹角为θ,小球B与竖直杆间的弹力为F1,地面对底座的弹力和摩擦力分别为F2和F3.现在将底座向右侧移动少许,重新达到平衡后,下列说法正确的是( )| A. | θ变小 | B. | F1变大 | C. | F2 变小 | D. | F3不变 |
13.关于传感器,下列是中正确的是( )
| A. | 半导体热敏电阻常被用作温度传感器,其温度越高,阻值越大 | |
| B. | 电饭锅应用了温度传感器,它的主要元件是感温铁氧体 | |
| C. | 电熨斗装有双金属片,应用了力传感器 | |
| D. | 计算机的鼠标器主要应用了力的传感器 |
17.一列火车从张掖开往北京,下列叙述中,指时间的是( )
| A. | 火车在早上5点20分从张掖出发 | B. | 列车在下午13点20分到达北京站 | ||
| C. | 列车在9点45分到达中途的南京站 | D. | 列车共运行了32小时 |
 在用如图所示的装置做“研究平抛物体运动”的实验时,实验简要步骤如下:
在用如图所示的装置做“研究平抛物体运动”的实验时,实验简要步骤如下: 如图所示,一个由某种透明物质制成的三棱镜,顶角θ=30°,∠C=90°,一束绿光射向AC面,经过AB面射出以后的光线偏离原来方向15°,则该介质对绿光的折射率为
如图所示,一个由某种透明物质制成的三棱镜,顶角θ=30°,∠C=90°,一束绿光射向AC面,经过AB面射出以后的光线偏离原来方向15°,则该介质对绿光的折射率为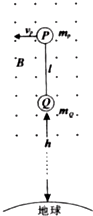 近期《科学》中文版的文章介绍了一种新技术--航天飞缆,航天飞缆是用柔性缆索将两个物体连接起来在太空飞行的系统.飞缆系统在太空飞行中能为自身提供电能和拖曳力,它还能清理“太空垃圾”等.从1967年至1999年17次试验中,飞缆系统试验已获得部分成功.该系统的工作原理可用物理学的基本定律来解释.如图为飞缆系统的简化模型示意图,图中两个物体P,Q的质量分别为mP、mQ,柔性金属缆索长为L,外有绝缘层,系统在近地轨道作圆周运动,运动过程中Q距地面高为h.设缆索总保持指向地心,P的速度为vP.已知地球半径为R,地面的重力加速度为g.
近期《科学》中文版的文章介绍了一种新技术--航天飞缆,航天飞缆是用柔性缆索将两个物体连接起来在太空飞行的系统.飞缆系统在太空飞行中能为自身提供电能和拖曳力,它还能清理“太空垃圾”等.从1967年至1999年17次试验中,飞缆系统试验已获得部分成功.该系统的工作原理可用物理学的基本定律来解释.如图为飞缆系统的简化模型示意图,图中两个物体P,Q的质量分别为mP、mQ,柔性金属缆索长为L,外有绝缘层,系统在近地轨道作圆周运动,运动过程中Q距地面高为h.设缆索总保持指向地心,P的速度为vP.已知地球半径为R,地面的重力加速度为g.