题目内容
18.汽车以10m/s的速度在平直公路上行驶,突然发现前方有一辆自行车正以4m/s的速度匀速骑行,若汽车立即以为6m/s2的加速度开始减速,没有碰上自行车.求汽车驾驶员发现自行车时两车的距离.设驾驶员的反应时间是0.5s.分析 当汽车速度减小为自行车的速度时,若不会撞上自行车,则不会与自行车相撞,临界情况时速度相等时恰好不相撞,结合速度时间公式和位移公式求出关闭油门时汽车离自行车的最小距离.
解答 解:设汽车司机看见自行车时相距为x0,反应后关闭油门,当两者速度相等时距离最近,此时若不相撞,便不会相撞;
设经时间t两者速度相等,则有v2=v1-at,
得:t=$\frac{{v}_{1}-{v}_{2}}{a}=\frac{10-4}{6}s=1s$;
这段时间内汽车的位移:${x}_{1}={v}_{1}{t}_{0}+{v}_{1}t-\frac{1}{2}a{t}^{2}$;
带入数据得:x1=12m;
自行车的位移:x2=v2(t0+t)=4×(0.5+1)=6m;
故汽车司机看见自行车时,两者相距至少为:x0=x1-x2=12-6=6m;
答:司机看见自行车时,汽车离自行车距离至少为6m.
点评 速度大者减速追速度小者,速度相等前,两者的距离逐渐减小,若不相撞,则速度相等后,两者的距离逐渐增大,可知临界情况时速度相等时,恰好不相撞.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
8.一根长为0.1m的电流为1A的通电导线,在磁场中某处受到的安培力大小为0.4N,则该处的磁感应强度为( )
| A. | 一定等于4T | B. | 大于或等于4T | C. | 小于或等于4T | D. | 可能为0 |
9.一个静止的质点,在0~8s内沿一条直线运动,加速度a随时间t的变化图线如图所示.则质点在( )

| A. | 第1s末速度方向改变 | B. | 第8s末速度为4m/s | ||
| C. | 2s内物体的位移为2.5m | D. | 第8s末回到原出发点 |
6.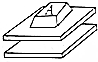 如图所示,有的计算机键盘的每一个键下面都连有一块小金属片,与该金属片隔有一定空气的是另一块小的固定金属片,这两块金属片组成一个平行板电容器.当键被按下时,此小电容器的电容发生变化,与之相连的电子线路就能检测到是哪个键被按下了,从而给出相应的信号.设当键未按下时两金属片的距离为d,电容为C;当键被按下时,此平行板电容器的电容发生变化,当变化量为△C时,电子线路恰能检测出必要的信号,则键至少要被按下的距离为( )
如图所示,有的计算机键盘的每一个键下面都连有一块小金属片,与该金属片隔有一定空气的是另一块小的固定金属片,这两块金属片组成一个平行板电容器.当键被按下时,此小电容器的电容发生变化,与之相连的电子线路就能检测到是哪个键被按下了,从而给出相应的信号.设当键未按下时两金属片的距离为d,电容为C;当键被按下时,此平行板电容器的电容发生变化,当变化量为△C时,电子线路恰能检测出必要的信号,则键至少要被按下的距离为( )
 如图所示,有的计算机键盘的每一个键下面都连有一块小金属片,与该金属片隔有一定空气的是另一块小的固定金属片,这两块金属片组成一个平行板电容器.当键被按下时,此小电容器的电容发生变化,与之相连的电子线路就能检测到是哪个键被按下了,从而给出相应的信号.设当键未按下时两金属片的距离为d,电容为C;当键被按下时,此平行板电容器的电容发生变化,当变化量为△C时,电子线路恰能检测出必要的信号,则键至少要被按下的距离为( )
如图所示,有的计算机键盘的每一个键下面都连有一块小金属片,与该金属片隔有一定空气的是另一块小的固定金属片,这两块金属片组成一个平行板电容器.当键被按下时,此小电容器的电容发生变化,与之相连的电子线路就能检测到是哪个键被按下了,从而给出相应的信号.设当键未按下时两金属片的距离为d,电容为C;当键被按下时,此平行板电容器的电容发生变化,当变化量为△C时,电子线路恰能检测出必要的信号,则键至少要被按下的距离为( )| A. | $\frac{dC}{C+△C}$ | B. | $\frac{dC}{C-△C}$ | C. | $\frac{d△C}{C+△C}$ | D. | $\frac{d△C}{C-△C}$ |
13.甲用手将物体举高1m,乙用机械效率为70%的动滑轮将此物提高1m,则下列说法正确的是( )
| A. | 甲比乙省力,两人做的有用功相等 | B. | 甲比乙省力,两人做的总功相等 | ||
| C. | 乙比甲省力,两人做的有用功相等 | D. | 甲比乙省力,两人做的总功相等 |
4.一个热气球以40m/s的速度匀速竖直上升,在某时从气球上落下一个重物,已知重物离开时热气球距离地面的高度为100m,不计重物所受的空气作用力,重力加速度g=10m/s2.则下列说法正确的有( )
| A. | 重物还能上升2s,然后落下 | B. | 重物离地最大高度为180m | ||
| C. | 再经过2$\sqrt{5}$s,重物落地 | D. | 再经过10s,重物落地 |
9.有下列几种情景,请根据所学知识选择对情景的方向和判断正确的说法( )
| A. | 点火后即将升空的火箭,因火箭还没运动,所以加速度一定为零 | |
| B. | 高速公路上沿直线高速行驶的轿车为避免事故紧急刹车.因轿车紧急刹车,速度变化很快,所以加速度很大 | |
| C. | 高速行驶的磁悬浮列车,因速度很大,所以加速度也一定很大 | |
| D. | 匀速飞行的高空侦察机,尽管它的速度能够接近1000m/s,但它的加速度为零 |
 如图所示,质量为0.78kg的金属块放在水平桌面上,在与水平成37°角斜向上、大小为3.0N的拉力F作用下,以4.0m/s的速度向右做匀速直线运动.已知sin37°=0.60,cos37°=0.80,g取10m/s2.
如图所示,质量为0.78kg的金属块放在水平桌面上,在与水平成37°角斜向上、大小为3.0N的拉力F作用下,以4.0m/s的速度向右做匀速直线运动.已知sin37°=0.60,cos37°=0.80,g取10m/s2. 如图所示,一束截面为圆形半径为R的平行单色光,垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形亮区,已知玻璃半球的半径为尺,屏幕S到球心的距离为d(d>3R),不考虑光的干涉和衍射,玻璃对该光的折射率为n,求
如图所示,一束截面为圆形半径为R的平行单色光,垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形亮区,已知玻璃半球的半径为尺,屏幕S到球心的距离为d(d>3R),不考虑光的干涉和衍射,玻璃对该光的折射率为n,求